Kopernikuszt Rheticus (1514-1574) osztrák származású matematikus vette rá, hogy művét mégis engedje kinyomtatni. Ez a Rheticus maga is foglalkozott a Mars mozgásával, de nem sokra jutott. Kepler egy helyütt ezt írta róla: „Az atyáink idejében élt Georg Joachim Rheticusról, Kopernikusz nagyhírű tanítványáról… a következő történetet mesélik: Amikor egy ízben belezavarodott a Mars pályájának számításába, és képtelen volt továbbhaladni, végső elkeseredésében őrangyalához folyamodott tanácsért. A goromba angyal megragadta Rheticus haját, és fejét többször a szoba menynyezetéhez verte, és mindannyiszor hagyta, hogy a tudós a padlóra zuhanjon; a kezelés közben pedig ezt a kinyilatkoztatást tette: Ime a Mars mozgása! A szóbeszédnek éles nyelve van… Azt azonban könnyen elhiszi az ember, hogy Rheticus a munkában és a töprengésben megrekedve, haragjában maga verte a falba a fejét."
Johannes Kepler (1571-1630) fiatal kora óta foglalkozott a bolygópályák kérdésével. A kopernikuszi világképből indult ki, vagyis a bolygópályákat a Nap körüli köröknek gondolta. A heliocentrikus világkép még korántsem volt kétséget kizáróan bizonyítva, de mellette szólt néhány megfigyelés; így pl. hogy a Mars (de a többi bolygó is) erősen változtatja látszó fényességét. Ezt legegyszerűbben úgy lehetett magyarázni, hogy változik a bolygó távolsága a Földtől. A változást a geocentrikus világkép lényegében nem tudta értelmezni, a heliocentrikus elképzelés alapján viszont természetesen következik.
Arra a kérdésre, hogy miért épp akkorák a pályasugarak amekkorák, és miért éppen hat bolygó van, Kepler egy meglehetősen fantasztikus ötlet alapján próbált felelni. Föltette, hogy a hat bolygó pályasugarának megfelelő méretű gömbhéjak közé éppen befér az öt szabályos test (a Merkúr és a Vénusz közé oktaéder, a Vénusz és a Föld közé ikozaéder, aztán dodekaéder, tetraéder és végül kocka). Ezt az elképzelést a Mysterium Cosmographicumban közölte. Maga is rájött azonban, hogy az így kapott pályasugarak nem egyeznek a bolygók megfigyelt pályaadataival, és az eltérést mindenféle mesterkedéssel igyekezett eltüntetni. Könyve azonban tartalmaz egy sokkal érdekesebb ötletet is: a bolygókat a Napból kisugárzó valamiféle erő tartja meg pályájukon, és ez a hatás a Naptól mért távolsággal csökken. A tudomány történetében talán ez volt a gravitációs törvény első megsejtése. (Kepler később még közelebb jut az általános gravitáció fölismeréséhez, de a legutolsó lépést már nem tudja megtenni, az Newtonra marad.)
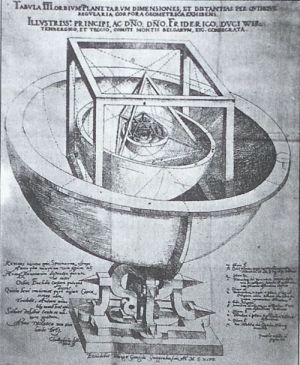
A bolygópályák távolságarányát szemléltető nevezetes ábra a Mysterium cosmographicumból.
Kepler kiváló matematikus volt, sokat foglalkozott pl. a kúpszeletekkel; az analízis egyik úttörőjeként terület- és térfogatszámítási feladatokat is tanulmányozott. Ebben nem törekedett teljes matematikai precizitásra, inkább Arkhimédész gondolatmenetének gyökerei érdekelték. Munkájának egy fontos eredménye volt a söröshordók legcélszerűbb alakjának meghatározása (1615); egy másik a II. Kepler-törvény (1609).
A bolygópályákra vonatkozó elméletének továbbfejlesztésére, illetve új elmélet kidolgozására mindaddig nem volt mód, amíg nem álltak rendelkezésére pontosabb adatok a bolygók észlelt pozícióiról. Ezekhez akkor jutott hozzá, amikor Tycho Brahe (1546-1601) meghívására 1601-ben Prágába költözött és Tycho egyik segédje lett. Tycho ugyanis akkor már hosszú évtizedek óta végezte igen pontos bolygó-észleléseit, mert felismerte, hogy ezek nélkül nem lehet a bolygó megoldásához közelebb jutni. Tycho azonban nem volt kopernikánus, sőt megvetette a lengyel kanonokot, mivel az „csupán" elméleti kutató volt, észleléseket alig végzett. Tycho felelevenítette egy régi görög püthagoreus csillagász, Hérakleidész elméletét, amely szerint a világ közepe a Föld, körülötte kering a Nap és a Hold; a bolygók viszont a Nap körül keringenek.
Alig érkezett meg Kepler Prágába, a két csillagász összeveszett. Természetük olyannyira különböző volt, hogy együttműködésükre alig volt remény. Tycho azonban fél év múlva meghalt, s Rudolf császár Keplert nevezte ki utódjául. Tycho örökösei ugyan számtalan nehézséget támasztottak, de végül Keplernek sikerült megszereznie Tycho legfontosabb hagyatékát, az annyira áhított adatokat.
Kepler megérkezésekor Tycho és egyik kedvenc munkatársa, Longomontanus (1564-1647) már rég bajlódott a Mars pályájának vizsgálatával, de sehogyan sem boldogultak vele. Kepler magabiztosan fogadást kötött, hogy ha rá bízzák a Marsot, nyolc nap alatt megoldja a problémát. Így hát Longomontanus a Holddal kezdett foglalkozni, Kepler pedig nekiláthatott a marspálya meghatározásának. A fogadást elvesztette ugyan, mégis szerencséje volt, hiszen az akkor ismert bolygók közül a Mars pályája tér el legjobban a körtől (hiszen a kutatók mindaddig épp ezért nem tudtak vele mit kezdeni), tehát az eltérés kimutatása és tanulmányozása e bolygó esetén volt viszonylag a legegyszerűbb. Így is több évre munkát adott Keplernek, de a csillagász végül győzedelmeskedett. Munkáját egy levelében a görög mondabeli hős, Héraklész egyik feladatához, Augiász istállójának kitakarításához hasonlította.
Kepler is úgy fogott hozzá a feladathoz, mint eddig mindenki más: megpróbálta az észlelt adatokat összeegyeztetni a feltevéssel, hogy a bolygó körpályán kering. Így azonban nem jutott eredményre ő sem, tehát megállapította: új utat kell keresnie. Elődeitől eltérően Kepler mindjárt a jelenségek okain, magyarázatán is gondolkodott, ami pedig új, mai fogalmaink szerint fizikai jellegű megfontolásokhoz vezetett; végső soron ez tette lehetővé a sikert.
Először is bebizonyította, hogy a bolygó pályasíkja áthalad a Napon, és az ekliptikával mintegy 1°50′ szöget zár be. A napközéppontú körpálya helyett, még mindig elődei nyomán haladva, föltette, hogy a körpálya geometriai középpontján kívül van egy pont (az ekváns), ahonnan nézve a Mars mozgása egyenletesnek látszik, és egy másik pont ugyanazon átmérő mentén, amelyben a Nap helyezkedik el. Azért van szükség az ekvánsra – érvelt -, mert a Nap nem a pálya középpontjában áll, s mivel a Napból ered a bolygót mozgató hatás, ennek erősebben kell érvényesülnie, amikor a bolygó napközelben van. Mozgása tehát nem egyenletes, ha a pálya középpontjából nézzük. Következő lépésben ezt a két föltételezett pontot határozta meg a Tychótól örökölt adatok felhasználásával. Olyan pozícióadatokból indult ki, amelyek a Mars oppozícióira vonatkoztak. Öt évi munkával sikerült a célt elérnie, közben néhány lényeges számítási hibát is elkövetve, melyek azonban szerencsére lényegében kompenzálták egymást. Kiszámította a marspálya sugarát és az említett két pont helyét; ezek alapján az észlelt és a számított oppozíciók mintegy két szögperccel tértek el csupán. Az oppozíciókon kívüli helyzetekre azonban nem kapott helyes eredményeket, s a modell változtatásával a legjobb esetben is még mindig nyolc ívperc hiba lépett föl. Tycho pontos megfigyeléseihez képest ez a hiba megengedhetetlen, a rendszer tehát hibás – állapította meg Kepler.
Megvizsgálva a bolygó sebességének változását, fölismerte a területi sebesség állandóságának elvét (ma impulzusmomentum-megmaradás néven ismerjük) a Mars mozgása esetére. Ez lett a II. Kepler-törvény. Sokkal nehezebb volt a pálya alakjának meghatározása. Tulajdonképpen nem is lett volna olyan nehéz, de Kepler, mint minden kortársa, annyira a régi, misztikával és irracionális elemekkel átszőtt világképben tanult meg gondolkodni, hogy az egyre világosabban kirajzolódó evidencia ellenére sem volt képes felismerni az ellipszist. Mindenféle furcsa görbét próbált ki, például a perihéliumban hegyesebb, aphéliumban laposabb tojás alakút; de természetesen nem volt képes ezeket a megfigyelt adatokhoz illeszteni. Többször is eljutott az ellipszishez, míg végre, egy hirtelen (matematikai jellegű) fölismerés nyomán rádöbbent a megoldásra. Rájött, hogy a pályagörbe ellipszis!
A pálya megszerkesztését egy rá jellemzően zseniális ötlet alapján végezte el. Először is szüksége volt a Mars sziderikus keringési idejére, amit akkoriban még nem ismertek, mivel az a Nap körül keringő Föld mozgása miatt közvetlenül nem mérhető. Tycho megfigyeléseiből azonban pontosan kiderült a bolygó szinodikus keringési ideje: két oppozíció közt kb. 780 nap telik el.
Ismerve mármost a Föld sziderikus és a Mars szinodikus keringési idejét, könnyen ki lehet számítani a Mars sziderikus keringési idejét is. Tekintsük ugyanis ismét a bolygók mozgását egyenletes körmozgásnak! Képzeljük el, hogy éppen oppozícióban van egy külső bolygó, pl. a Mars! Legyen a Föld keringésének szögsebessége ω1 = 2π/T1 , ahol T1 = a Föld sziderikus keringési ideje, vagyis 1 év; legyen a külső bolygó keringésének szögsebessége ω2 = 2 π / T2 , és itt T2 a külső bolygó keresett sziderikus keringési ideje. Tudjuk az elemi fizikából, hogy a vezérsugár szögelfordulása t idő alatt φ = ω t, és keringés közben a Föld gyorsabban halad a külső bolygónál, tehát akkor következik be ismét az oppozíció, amikor a Föld egyszer „lekörözi" a külső bolygót, azaz amikorra egy körrel többet futott be, mint amaz. A két bolygó vezérsugara által megtett szögelfordulás különbsége tehát ω1 t – ω2 t = 2 π. Beírva ebbe az ω1 és ω2 definícióját, majd 2 π t-vel elosztva az egyenletet, kapjuk: 1 / T1 – 1 / T2 = 1 / t .
Ebbe az ismert T1 és t értéket beírva ki tudjuk számítani a keresett T2-t. Esetünkben (két tizedes pontossággal számolva) T1= 365,24 nap, t= 779,86 nap; ezekkel T2= 686,98 nap, azaz ennyi a Mars sziderikus keringési ideje.
A Mars tehát kb. 687 nap elteltével pályája ugyanazon pontjára jut vissza, a Föld azonban nem. Ezért a Földről a bolygó a két időpontban nem ugyanazon csillagok irányában látható, bár a térben ugyanott van. Papíron meg tudjuk szerkeszteni mindkét időpontra a bolygó látóirányát; s a két félegyenes metszéspontja megadja a bolygó valódi térbeli helyzetét. Ez volt az a zseniális ötlet, amely Keplert képessé tette a marspálya megszerkesztésére. Tycho mért adatai közül sok olyan párt lehetett kiválasztani, amelyek 687 napnyi különbséggel készültek. Minden ilyen pár megadott egy-egy pontot a pályán, amely így szépen kirajzolódott a papíron. Miután, lapultságának egy bizonyos mértéke alapján, fölismerte a görbét, Keplernek már csak meg kellett fogalmaznia a törvényt: a Mars pályája ellipszis, melynek egyik gyújtópontjában áll a Nap. S ha a Mars pályája ellipszis, feltehetőleg a többi bolygóé is az!
Az első két törvényt Kepler az 1609-ben megjelent Astronomia nova c. könyvében közölte, amelyben módszert is adott a bolygóhelyzetek előre megadására. Ugyanitt az égimechanikában ma is használatos ún. Kepler-egyenletet is leírta.
További évtizedes munkával számos matematikai összefüggést talált a Naprendszer tagjainak mozgásában. Ezek egy része véletlen, más részét ma rezonancia effektusként ismerjük, megint mások a gravitációs törvény következményei. Vannak köztük mai szemmel nézve eléggé furcsák is, mint pl. a bolygók „dallamai", amelyek szerinte a püthagoreusok által „szférák zenéjé"-nek nevezett állítólagos harmóniáknak felelnek meg, és amelyeket Kepler gondosan lekottázott. Mindezt az 1619-ben kiadott Harmonices mundiban találhatjuk meg. A kötetben a legfontosabb eredményt Newton találta meg, ezt ma III. Kepler-törvény néven ismerjük: a bolygók keringési idejének négyzete úgy aránylik egymáshoz, mint pályaellipszisük fél nagytengelyének köbe. Az összefüggés nemcsak a Naprendszer bolygóira, hanem bármely közös gravitációs vonzócentrum körül keringő testek rendszerére is igaz.
Ez a törvény, akárcsak az első kettő, Keplernél egyszerű tapasztalati törvény, indokolás nélkül. Az indoklást majd Newton adja meg, levezetve mindhármat a mechanika alaptörvényeiből és a gravitációs törvényből. Sőt Newton e törvényeket általánosítja is; munkája nyomán ma nemcsak a Naprendszer, hanem pl. a kettőscsillagok vizsgálata során is használjuk őket (gondoljunk pl. az ún. dinamikus parallaxis meghatározásra!).
Keplert ezek a fölfedezései a tudománytörténet legnagyobbjai közé emelik. Rajta kívül talán csak Einstein volt képes arra, hogy fölismerve saját világképének hibás voltát, túllépve rajta, új, korát messze megelőzően modern világképet dolgozzon ki.
A Meteor 2003/7-8. számában megjelent cikk internetes változata











