
Hell Miksa rövid életrajza
Hell Miksa 1720. május 15-én született Selmecbányán, a ma Szlovákiához tartozó Banská Štiavnica-n. Eredetileg családneve Höll volt, de ezt 1760-ban, császári csillagász korában Hellre változtatta. Apja kiváló bányamérnök volt, több találmánnyal járult hozzá a selmeci bányászat fejlődéséhez. 23 gyermeke közül Miksa vitte a legtöbbre, de másik két fia, József és Ignác Kornél is kitűnő szakember volt a maga szakterületén, a bányászatban.
Hell Miksa középiskolai tanulmányait szülővárosa gimnáziumban végezte. Ezután 1738-ban Besztercebányán belépett a jezsuita rendbe. Két noviciátusi évét Trencsénben töltötte, ahol kivált a rendi tanulmányok iránti érdeklődésével. 1741-től Bécsben tanult, először filozófiát, majd természettudományokat. Hamar megszerezte rendi elöljáróinak megbecsülését, s társainak felügyelője (manuductor) lett. 1743-tól matematikát és csillagászatot tanult, Joseph FRANTZ csillagász tanítványaként. Ebben az időszakban lefordította latinra J. CRIVELLI olasz nyelvű matematikai munkáját. Ezt kibővítette, javította, és 1745-ben kiadta (Elementa, 1745). 1745-ben már Joseph FRANTZ segédjeként is tevékenykedett és saját csillagászati megfigyeléseket is közölt és közreműködött a természettudományi múzeum rendezésénél.
1745-ben a rend lőcsei gimnáziumába került tanárnak, majd 1748 és 1752 közt Bécsben hallgatott teológiát. Itt írt társai számára egy tudományos kisenciklopédia-félét (Adiumentum memoriæ manuale chronologico-genealogico-historicum), melyet különböző országokban többször is kiadtak.
1751-ben szentelték pappá, és a harmadik próbaévre Besztercebányára helyezték. Innen irányította a nagyszombati csillagda építését, majd Kolozsvárra utazott tanárnak és az ottani csillagda építésének irányítására. Sokféle teendője mellett még katonai lelkész is volt.
A már tudományos nevet szerzett fiatal jezsuitát Mária Terézia 1755-ben kinevezte császári királyi csillagásznak (Astronomus Cæsareo-Regius) a bécsi csillagdába. Itteni sokféle kötelezettségének is (tanítás, a felszerelés karbantartása és fejlesztése, csillagászati észlelések, csillagászati évkönyv kiadása, előadások tartása stb.) igen lelkiismeretesen tett eleget. Kapcsolatba került a kor legnagyobb csillagászaival, akik megfigyelései gondossága miatt nagyra becsülték. Közben további magyarországi csillagvizsgálók alapítását is segítette, így az egri és a budai obszervatórium tervezésében és felszerelésük beszerzésében is részt vett.
VII. Keresztély dán király a Vénusznak a Nap előtti 1769. jún. 3-i átvonulása megfigyelésére Vardöbe hívta meg Hellt. Hell és segítője, SAJNOVICS János 1768 ápr. 28-án indultak útnak; sokrétű természettudományos megfigyelést végeztek mind útjuk során, mind pedig Vardöben. Eközben Hell kipróbálta a földrajzi szélesség (tkp. a sarkmagasság) mérésére feltalált igen fontos (és igen pontos) módszerét, amely ma Horrebow-Talcott-eljárás néven ismeretes és használatos. Az útjuk céljául szolgáló mérést nagy szerencsével sikeresen elvégezték. (Közben Sajnovics fölfedezte a magyar-lapp nyelvrokonságot.) Ez az expedíció tette Hell nevét világhírűvé.
A jezsuita rend 1773-as eltörlése miatt megszűnt a rend részéről Hellnek nyújtott anyagi és szellemi támogatás. Hell a világi papság kötelékébe lépett, de mindvégig reménykedett rendje újjáéledésében (amit azonban már nem érhetett meg). Ha nem is zavartalanul, de folytatta sokoldalú tudományos kutatásait többek között a néprajz, földrajz, történelem, teológia, fizika tárgyköreiben —természetesen a csillagászat mellett. 1774-ben a naptár ügyében nyújtott be egy tervezetet a bécsi udvarhoz. Ennek eredményeképpen egy 1776-os császári rendelet alapján Hell gondoskodhatott egy csillagászati naptár kiadásáról.
Az egyre szaporodó, egyedül végzett munka aláásta egyébként sem szilárd egészségét. 1792 tavaszán meghűlt, s tüdőgyulladásából már nem gyógyult fel. 1792. április 14-én, 72 éves korában hunyt el Bécsben.
Höll (Hell) Miksa kolozsvári munkássága
A jezsuita rend Kolozsváron a XVI. század második felében indította el az oktatást a Báthory Egyetemen, amelynek alapítólevelét Báthory István Erdély fejedelme és Lengyelország királya 1581. május 12-én keltezte a lengyelországi Vilnában. A XVIII. század második felére az egyetem vezetői úgy találták, hogy a természettudományi részleget és ezen belül a csillagászat oktatását is erősíteni kell. Erre a munkára olyan rendtagot kerestek, akinek ezen a téren már megfelelő ismeretei voltak, és feltehető volt, hogy tudását a kolozsvári egyetemen az alkalmazott tudományos csillagászati ismeretek tanításában gyümölcsöztetni tudja. Így esett a választás Hell (ekkor még Höll) Miksára. Hell alapvető feladata egy csillagda létrehozása volt (Heinrich, 1978).

2. ábra. Kolozsvár látképe 1759-ből. Szakál János rézmetszete (Heinrich, 1978).
Amint a bemutatott rövid életrajzból is kitűnik, Hell a bécsi tanulmányai alatt alapos csillagászati elméleti és gyakorlati ismeretekre is szert tett, amit már korábban a nagyszombati csillagvizsgáló építésének irányításánál is gyümölcsöztetett. Amikor Kolozsvárra került, csillagászati megfigyeléseit — akárcsak a korábban itt oktató Jánosi Miklós — csak a magánlakásán berendezett kis csillagdájában végezhette, így komolyabb csillagászati észlelésekre nem nyílt alkalma. Erről Döbrentei Gábor (1815) így ír: „Hell egy Múzeum’ ‘s Observatórium alapját veté-meg, azon szobákban, melyekben most a’ tartománybeli Számláltató-Tisztség van …”.


3. ábra. A kolozsvári egyetem régi épületének tanári lakásai, ahol Höll Miksa végezte megfigyeléseit (Heinrich, 1978), valamint az első kolozsvári csillagda refraktora, amelyet napjainkban a Báthory Líceum fizikumának szertárában őriznek.
A közel hároméves kolozsvári működése alatt Höll maradandót főként a matematika terén alkotott. 1755-ben a kolozsvári akadémiai nyomdában adja ki Elementa mathematica naturali philosophiae ancilliantia (A természetfilozófia leányának, a matematikának elemei) című könyvét (Höll, 1755a). Hell egy átfogó, több kötetes matematikai mű megírását tervezte, de Bécsbe való áthelyezése után a csillagászati elfoglaltságok miatt már nem jutott ideje a sorozat folytatására. Így csupán a Kolozsváron megírt első kötet jelent meg: Elementa Aritheticae nuericae, et literalis seu Algebrae, (A numerikus és betűszámtan, vagyis az algebra elemei) vagyis az aritmetikáról és az algebráról szóló könyv, akkoriban sikernek számító ezer példányban (4. ábra, Heinrich, 1978). A könyv sikerét bizonyítja, hogy később több alkalommal is újból kiadták Lengyelországban, majd Bécsben két alkalommal is (1761, 1773).
A könyv bevezetőjében Hell elmeséli, hogy tíz évvel korábban, amikor filozófiahallgatók számára Crivellius Algebrájának kiadását gondozta, eszébe sem jutott, hogy valaha is matematika könyvet írjon, főként, hogy időközben megjelent Erasmus Froelich: Introductio facilis in Mathesim, ad usum tyronum Phylosophiae Provinciae Austriae S. J. Viena, 1764 könyve is. Majd így folytatja: „De mivel megváltozott akadémiáink Tanulmányi Szabályzata, a Matematikai Kollégiumok nyilvános előadásaira megállapított Tanrend egy olyan könyvet követelt meg, amelyben az aritmetika, algebra, geometria, trigonometria és mind elméleti és gyakorlati architektúra alapelvei, valamint az általános használatra alkalmas ismereteket úgy tárgyalják, hogy az először is alkalmas legyen a hallgatók számára, sok ismeretet tartalmazzon, mentes legyen a fölös tehertől, nagy gonddal megválasztott sok példát tartalmazzon, és hasznos legyen főként azok számára, akik az aritmetikának még az alapjait sem ismerik”. Hell művével hozzá akart járulni hazája haladásához, főként a polgári lakóságnak segítve.
Hell tankönyve Jánosi Miklós: Trigonometria plana et spherica cum selectis ex Geometria et Astronomia problematis (Sík- és gömbháromszögtan, a mértanból és csillagászatból válogatott példákkal) Kolozsváron 1737-ben kiadott könyve után a második Erdélyben nyomtatott, eredeti jellegű matematika könyv.
A könyvben más szerzőktől átvett részek esetén idézi a forrást. A bevezetőjében köszönetet is mond neves mestereinek, Joseph FRANTZ-nak és Erasmus FROLICH-nek, kiemelve, hogy az elsőnek köszönheti teljes matematikai jártasságát, főleg a csillagászati és fizikai tárgyak terén, míg a másodiknak a matematikai elmélet terén. Hell, míg könyvének értékeit jezsuita tanítómestereinek tulajdonítja, addig az olvasót arra kéri, hogy az esetleges hibákért az ő sietségét és megfontolatlanságát okolja.
4. ábra. Höll Miksa Kolozsvárott 1755-ben megjelent matematika könyvének és példatárának címlapja.
A Bevezetőben továbbá ismerteti, hogy meglátása szerint mi a matematika, beszél a matematika módszeréről, majd sorra értelmezi a matematikusk által használt definíciók, posztulátumok, axiómák, tapasztalatok, hipotézisek, föltevések, bizonyítások, tételek, problémák, porismák vagy lemmák [segédtételek], korolláriumok [következmények] és scholia [megjegyzések] fogalmát. Íme egy kis ízelítő Hell értelmezéseiből Csaba György Gábor (1997) fordításában:
A matematika módszeréről
I. A matézis (görög szóval Mαθησιζ, tudomány, vagy antonomasiát alkalmazva disciplina) a mennyiség tudománya. Két fajtája a Tiszta és a Kevert matematika [mathesis pura et mixta]. A tiszta matematika a minden anyagitól mentes mennyiség tudománya, amelynek tárgya minden, ami megszámolható vagy mérhető; ide tartozik az algebra a numerikus aritmetikával együtt, valamint a tiszta geometria. Kevert matematikának mondják a matematikának azt a részét, amely fizikai anyaggal kapcsolatos; ilyenek a kevert geometria, a statika, mechanika, hidraulika stb. A tiszta matematika a legbiztosabb tudomány, a kevert viszont csak a matematikai forma szerint biztos, de nem az anyag szerint.
II. A matematikai módszer az a mód vagy valamely különleges eljárás, amelyet a matematika az igazságainak fölfedezésére, bizonyítására, átadására használ. Két részre osztható, éspedig az analitikus és a szintetikus módszerre. Az analitikus vagy szétbontó módszer az igazságok megtalálására, fölfedésére szolgál; a szintetikus vagy egyesítő pedig mindazt, amit az analízis segítségével találtunk, rendszerbe szedi, és egyik igazságot a másikhoz kapcsolja úgy, hogy egymástól mintegy összeláncolva függjenek; ez szolgál a matematika tételeinek átadására. Így a szintetikus módszer a következőket alkalmazza: I. Definíciók. II. Posztulátumok. III. Axiómák. IV. Tapasztalatok. V. Hipotézisek. VI. Föltevések. VII. Bizonyítások. VIII. Tételek. IX. Problémák. X. Porismák vagy Lemmák [segédtételek]. XI. Korolláriumok [következmények]. XII. Scholia [megjegyzések].
III. Definíció a megkülönböztető ismertetése vagy kifejtése a dolognak vagy névnek, amiről szó van. Pl. Szám az egységek rendezett sokasága.
IV. Posztulátumnak nevezzük azt, amiről megköveteljük, hogy valami másból könnyen levezethető legyen számunkra, hogy lehetséges. Pl. egy pontból a másikhoz egyenest húzni.
V. Axióma (Aξιωμα, hitelt érdemlő) az olyan igazság, amely kellően megértve a kifejezéseket, magától vagy a szavakból nyilvánvaló, vagy a természet fényében ismert. Pl. Az egész nagyobb, mint a rész.
Hell aritmetikája a következő részeket tartalmazza: Pars I. De natura, et Algorithmis numerorum vulgarium integrorum (A természetes egész számok és velük való műveletek); Pars II. De Logistica Decimali (A tizedes törtekkel való műveletek); Pars III. De reductione numerorum mixtorum, et animadversionibus in notas numericas (A vegyes számok egyszerűsítése és a számjegyekhez fűzött megjegyzések), (5. ábra).
A könyv sok érdekes adatot tartalmaz. Megtalálható benne az akkori pénzérmék és a különféle mértékegységek leírása. Például a korabeli Ausztria, Magyarország és Erdély területén egyaránt használatos polgári vagy kereskedelmi súlyegységeket az alábbi táblázatba foglalja össze:
1 Drachma, seu Quintl. 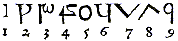 loth
loth
|
1 Semiuncia seu Loth |
4 |
||
|
1 Libra |
32 |
128 |
|
|
1 Centenarius |
100 |
3200 |
12800 |
A térfogat mérésére használt egységeket „az erdélyi bor mértékek” táblázatával mutatja be:
Quadrans
|
1 Sextarius seu media |
2 |
|||
|
1 Cupa seu mensura |
2 |
4 |
||
|
1 Urna Transylv. |
8 |
16 |
32 |
|
|
1 Urna Germ, in Trans. |
5 |
40 |
80 |
160 |
A táblázatot azzal a megjegyzéssel egészíti ki, hogy két erdélyi mérték tesz ki egy osztrák mértéket vagy egy magyar kupát. A korabeli osztrák mértékegységek ismeretében V. Marian következtetéseket von le az Erdélyben használt korabeli mértékegységek nagyságára (Marian, 1943/44).
Erdélyi vonatkozásai miatt is érdekes például az „Észrevételek a számjegyek jelölésével kapcsolatban” című rész, amely Csaba György fordításában:
„Figurák, avagy arab számjegyek, ahogyan ma használják őket:
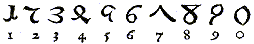
Az európaiak által egykor használt arab számjegyek:

Ez utóbbi arab számjegyekkel felírt évszámokat olvashatunk még ma is a legtöbb templomon és régebbi épületeken Ausztria és Magyarország-szerte, legfőképpen pedig Erdélyben azokon a helyeken, amelyeket Saxoniainak neveznek. Pl. az épületek építésének évét így olvassuk: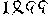 , vagy
, vagy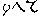 , vagy
, vagy  , amit senki más nem képes megérteni, mint csak az igen művelt “
, amit senki más nem képes megérteni, mint csak az igen művelt “
Az algebra fejezete a következő négy részből áll: Pars I. De Arithmetica literali, seu Algebra (A betűszámtan vagy algebra); Pars II. De Potentiis Quantitatum, et aerundem Radicibus (A hatványozás és a gyökvonás); Pars III. De Analysi speciosa, seu arte resolvendi Problemata Questiones quantumvis reconditas (Az algebrai analízis, vagy a szöveges feladatok és kérdések megoldásának módszere); Pars IV. De Proportionibus, Progressionibus, usu Regulae Aureae, Inventione Theorematum, ac Problematum (Aránypárok, haladványok, az aranyszabály, teorémák és feladatok megfogalmazása). Az eredeti latin címek fordítása Heinrich Lászlótól származik (Heinrich, 1978).

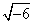
5. ábra. Hell algebra könyvének negyedik, bécsi kiadása és az aritmetika rész tartalomjegyzéke.
Az algebra elemei (III. rész) Csaba György Gábor fordításában például így kezdődik (Csaba, 1997):
Az algebra elemei III. rész
A szépséges Analysis, vagyis a problémák és
bármennyire elrejtett kérdések megoldásának
művészet
I. fejezet
Az Analysis egész művészetének axiómái, föltevései, általános gyakorlatai
I. DEFINÍCIÓ
212. Egyenlőségnek mondjuk az olyan algebrai kifejezést, amely az = jel közbeiktatásával kifejezi, hogy bizonyos, valahogyan adott mennyiségek egymás közt egyenlők, vagy egyenlők nullával: pl. ax + c = ab – d, vagy 3 + 5 – 2 = 6, vagy ax – ab = 0.
I. SCHOLION
213. Az egyenlőség kifejezése tehát kifejezi, hogy az összes együtt fölvett és az = jel elé helyezett mennyiség egyenlő az ugyanígy együtt vett és a = jel mögé helyezett mennyiség értékével, vagy ami ugyanaz, hogy a = jel bal oldalán álló mennyiségek egyenlők a = jel jobb oldalára tett mennyiségekkel, amint ez nyilvánvaló az előbb mondottakból.
II. SCHOLION
214. Az egyetlen közvetítő eszköz, amelyet az Algebra a mégoly elvont kérdések megoldására is használ, az egyenlet, avagy az egyenlőség kifejezése, az egész Analízis mestersége az egyenlőségek megtalálásában áll, és az adott egyenletnek egy ismeretlen mennyiségre (a mennyiségek egyenlőségének axiómái alapján történő) redukálásának mesterségében, úgy, hogy az egyenlet egyik oldalán csak egyetlen ismeretlen mennyiség szerepeljen, minden más, ismert vagy ismeretlen mennyiség nélkül, az egyenlet másik oldalán pedig tiszta ismert mennyiségek legyenek; amit hogy mi módon lehet helyesen elérni, a kérdések megoldásának általános mesterségét öt műveletre osztom, amelyekben ha a kezdő Analista jól begyakorolja magát, akkor neki semmi olyan nehéz probléma nem lehet, aminek megoldását, e műveletek segítségével, ne tudná megadni. Az Analista első művelete legyen: I. Az adott kérdés minden körülményének alapos vizsgálata, illetve az adott kérdés mibenlétének teljes, alapos megértése. II. A mennyiségeknek, mind az ismerteknek, mind az ismeretleneknek az ábécé betűivel való alkalmas jelölése. III. Az egyenlet megtalálása és felírása. IV. Az egyenlet redukálása, és V. A redukált egyenlet numerikus megoldása, vagy különösen alkalmas alakra hozása.
A Hell által használt algebrai jelek néhány apró kivétellel megegyeznek a ma is használatban levőkkel. Így, például az egyenlőség jeleként az (=) mellett használja a (::) és (¥) jeleket is, tehát nála a = b, vagy a :: b, a ¥ b. A szorzás jelölésére pedig az (x), valamint (.) és (,) jeleket használja (Marian 1943/1944).
Az algebra második részében, ahol a mennyiségek „hatványaival és gyökeivel„ foglalkozik, bevezeti az irracionális és imaginárius számokat is. Victor Marian észrevétele szerint itt sajnos hibásan adja meg az imaginárius számok szorzására vonatkozó szabályokat. Hell szerint ugyanis 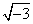 és
és 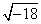 szorzata
szorzata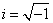 és méltatlankodva jegyzi meg, hogy hírneves itáliai szakemberek, köztük MARTINE is hibásan oktatják ezeket a szabályokat. Ez is mutatja, hogy ebben a korban valószínűleg nehezen igazodtak el a diákok az imaginárius mennyiségek világában, ha maga Hell is ilyen nehézségekbe ütközött. Nyilván Hell nem volt az egyedüli, akinek nem sikerült helyesen megbirkózni az imagináriusokkal. Ezt később az
és méltatlankodva jegyzi meg, hogy hírneves itáliai szakemberek, köztük MARTINE is hibásan oktatják ezeket a szabályokat. Ez is mutatja, hogy ebben a korban valószínűleg nehezen igazodtak el a diákok az imaginárius mennyiségek világában, ha maga Hell is ilyen nehézségekbe ütközött. Nyilván Hell nem volt az egyedüli, akinek nem sikerült helyesen megbirkózni az imagináriusokkal. Ezt később az imaginárius egység EULER általi 1777-beli bevezetése és annak GAUSS általi rendszeres használata tette hozzáférhetőbbé (Marian 1943/1944).
imaginárius egység EULER általi 1777-beli bevezetése és annak GAUSS általi rendszeres használata tette hozzáférhetőbbé (Marian 1943/1944).
Hell Kolozsváron elkezdte egy feladatgyűjtemény Exercitationum mathematicorum (matematikai feladatok) kiadását is, amelyet szintén több kötetesre tervezett. A korábban már ismertetett okok miatt azonban ennek is csak az első része jelent meg Exercitationes Arithmeticae (Aritmetikai feladatok) címen. Ebben az első aritmetikai gyakorlatokat közli és ígéri, hogy „ha az Istennek is fog tetszeni”, akkor majd a második kötetben közreadja a további részeket is. A „Fennvalónak” viszont úgy tetszett, hogy Hell az algebrai gyakorlatok helyett inkább csillagászati észleléseknek és azok közzétételének szentelje kiváló tehetségét és munkabírását. Hell ezen könyve is több kiadást megért, mindenütt az Elementa Arithmeticae numericae, et literalis seu Algebra című könyv mellékleteként, az első kiadásban 64 oldal terjedelemben (4. és 6. ábra).


6. ábra. Hell aritmetikai feladatgyűjteményének első oldalai.
Ezt a munkáját nemcsak a tanulóifjúságnak (usum privatum studioase juventutis), hanem a polgároknak és a kereskedőknek is szánta (ad usum civilem ac mercatorum applicatis declaratae). Itt különféle feladatokat találunk a hármasszabályra, a kamatszámításra, sőt a kamatos kamatszámításra is. Utóbbi esetben németül és magyarul is megadja a meghatározást (Heinrich, 1978).
Kolozsvárott 1775-ben további három kisebb terjedelmű matematikai munkát adott ki Hell: Compendia varia praxesque omnium operationum arithmeticarum (Az összes aritmetikai műveleteknek változatos és gyakorlati összefoglalása), A természeti bölcsészetet utánzó mértani elemek és Materia Tentaminis Mathematici (A matematika vizsgaanyaga) (Höll, 1755c). Az első két műről sajnos csak a Hellről szóló életrajzi írásokból tudunk. A harmadik, fennmaradt vizsgatétel részletes ismertetése olvasható Heinrich László munkájában (Heinrich, 1978).
Hell matematikai munkásságát többen is igen pozitívan értékelik. Így KÖLESEY Vincze Károly és MELCZER Jakab szerint Hell „Minden gondját arra fordította, hogy a’ Mathesisnak elsőbb fundamentomait kedvessé, világossá és könnyűvé tégye az ifjúság’ előtt, mellytől az előtt azok annyira irtóztak; eleikbe terjesztvén annak nagy béfolyását, és szükséges voltát, a’ közönséges világi életnek mindenféle állapotjaiban” (KÖLESEY– MELCZER, 1816). Döbrentei Gábor szerint „Különösen azon igyekezett , hogy a’ Mathesis’ kezdő fundamentumainak bizonyos interessét [itt: érdeklődést] adjon, ’s annak szárazságai által a’ tüzes ifjúi elmét el ne ijessze … A’ kik természeti rátermettségtől nem indítatnak, hamar megunják, ha a’ Tanító azon nincs, hogy a’ Mathesisnek a’ közönséges életbe való nagy béfolyását, sőt szükséges voltát meg nem mutatja, ’s példákkal nem világosítja. Hell … a’ tanításnak cselekedtető módját vette fel” (Döbrentei, 1817).
Hell Kolozsvárott nemcsak a matematikával foglalkozott, és nemcsak arra törekedett, hogy az új főiskolát a kísérleti fizika oktatásának minden kellékével felszerelje (Pinzger, 1927), hanem úttörő módon tanulmányozta a mágnesesség és az elektromosság közti összefüggés (Szabó, 1970). Ezen vizsgálódásairól a később Bécsben, 1762-ben megjelentetett 1762 Anleitung zum nutzlichen Gebrauch der künstlichen Stal-Magneten (Bevezetés a mesterséges acélmágnesek hasznos alkalmazásához) című könyvében számol be. A könyvben leírtak szerint az első két darab mesterséges mágnest egy kolozsvári református kollégiumi matematikatanártól kapta. Az ezekkel végzett kísérletek alapján erősödik meg benne az a meggyőződés, hogy a mágneses jelenségek nem mások, mint az elektromos anyagnak bizonyos fokú mozgásai. Kolozsvári tartózkodása alatt dolgozza ki a mágnesesség elektromos elméletét, de Bécsbe való áthelyezése ezt a munkát is megszakítja (Heinrich, 1978).
Hell érdeklődését nem kerülte el a mágnesek gyakorlati felhasználhatósága sem, kutatásait nemcsak tudományos, hanem gyakorlati céllal is végezte. Könyvének bevezetésében el is mondja, hogy ezen művét pontosan azért szerkeszti latin helyett német nyelven, mert nem tudósoknak, hanem kézműveseknek szánta. A felhasználhatóság egyik lehetséges területének Höll a gyógyítást gondolta, Kolozsváron sok kísérletet végezve erre vonatkozóan. Gyógyítási eljárásaiban nagy szerepe volt a szuggesztiónak is (Pinzger, 1927; Heinrich, 1978).
Hell Miksa, a bécsi császári csillagász
Hell Miksa 1755 szeptemberében hagyja el Kolozsvárt és költözik Bécsbe, ahol átveszi az elhunyt L. L. MARINONI császári udvari csillagász örökségét. Mária Terézia 1755. október 22-én nevezi ki a bécsi udvari csillagda igazgatójává és az egyetemi csillagászati tanszék vezetőjévé (Kisbán, 1942; Heinrich 1978). Hell Miksát új tisztségében a következő feladatok várták (Pitzger, 1920):
"Instructio Hell Miksa S. I. cs. kir. csillagász részére
Először: A csász. kir. csillagász a tanulmányaihoz tartozó teljes fölszerelésről és ennek időközönként történendő javításáról és megőrzéséről fog gondoskodni.
Másodszor: Kötelességeihez tartozik, hogy a bolygók pályájának megfigyelését végezze, és hogy ezáltal a megboldogult Marinoni által megkezdett és sok éven át folytatott Ephemerides Astronomicae-t tovább vezesse és mindent az arra rendelt könyvekbe beiktasson.
Harmadszor: A közönség a hold- és napfogyatkozások, csillagelfödések, üstökösök vagy más rendkívüli csillagászati jelenségek megfigyelésére… a kapura kifüggesztett táblákkal figyelmeztetendő és meghívandó.
…
Ötödször: Rábízzuk,… hogy teljesen mellőzze mindazt, amit a régieknek és köznépnek babonája és az alaptalan asztrológia… beszél.
1755. nov. 10."
Bécsi tevékenységének legértékesebb termékei a csillagászati évkönyvek: Ephemerides Astronomicae anii … ad meridianum Vinodobensem (A bécsi délkörre vonatkozó csillagászati táblázatok az … évre), amelynek évenként (1757–1786) megjelenő vaskos köteteiben nemcsak a szakcsillagászok számára találhatók érdekes adatok, hanem népszerű tudományos értekezések is (7. ábra). Az itt közölt értekezéseinek köszönhette Hell európai hírnevét (Papp, 1869).
Hell az Ephemerides Astronomicae évkönyveiben bőséges teret biztosított a hazai csillagászati megfigyeléseknek is. Külföldi kapcsolatait mutatja, hogy Lengyelország számára forgatható toronnyal ellátott kupolát tervezett. Ebből az alkalomból Stanislaus Augustus (Poniatowski Szaniszló Ágost) lengyel király az akkor élő csillagászok díszének nevezi Hellt (Döbrentei, 1817). Ugyancsak a Hell tervei alapján épül meg az egri és budai obszervatóriumok forgó kupolája. Az egri csillagvizsgálóban Hell 1776-ban személyesen vett részt az ott áthaladó észak-dél irányú meridiánvonal (délkör) kimérésében (Heinrich, 1978).
Hell évkönyveit egész Európában nagy érdeklődéssel várták. Fennmaradt annak az emléke, hogy a neves francia tudós D. Bernoulli, valamint a kor vezető csillagdái (a greenwichi és a szentpétervári) is sürgették a kiadványok megküldését (Heinrich, 1978). Éppen nemzetközi hírnevének köszönhetően választotta VII. Keresztély, Dánia és Norvégia királya Hell Miksát az 1769-i Vénusz-átvonulás megfigyelésére.

7. ábra. A Hell által szerkesztett Csillagászati évkönyvek első kötetének címlapja, 1577-ből.
A Vénusz a Földről nézve 243 évenként négyszer elvonul a Nap korongja előtt. Ezek az átvonulások nem csupán érdekes csillagászati eseményt jelentenek, hanem — mint arra fél évszázaddal Hell előtt Halley is rámutatott — segítségével meghatározható a Csillagászati Egység, azaz a Nap–Föld középtávolság pontos értéke.
Érthető lelkesedéssel készültek tehát a csillagászok Európa-szerte e jelenség megfigyelésére. VII. Keresztély dán király felkérte Hellt, hogy ő vezesse a legészakabbra induló expedíciót és Vardö szigetén figyelje meg az átvonulást. Hell a megbízást elfogadta és 1768. április 28-án útnak indult Lappföldre. Kísérője és munkatársa, a nyelvész és csillagász Sajnovics János az indulást megelőzően Bécsben a királyi párnál tett látogatásukról így írt naplójában:
"… Mindketten elmenénk az udvarhoz. Hell mindenféléről beszélt, végre megkérdeztetvén, hogy maga teszi-e meg a nagy utat, azt felelé, hogy útitársa kint várakozik s csak Felséged engedelmét várja, hogy lábaihoz borulhasson…
A császárné rövid beszélgetés után így szólt:
Hell és Sajnovics több hónapig tartó út után szerencsésen megérkezett Vardöbe, ahol kis csillagvizsgálót építettek a megfigyelésekhez. Míg a nagy napra vártak, Hell számos megfigyelést végzett a sarkkörön túli területek éghajlatáról, a tengerről és a sarki fényről, valamint kipróbálta a földrajzi szélesség (tkp. a sarkmagasság) mérésére feltalált módszerét, amely ma Horrebow-Talcott-eljárás néven ismeretes és használatos. Kísérőtársa és segítője, Sajnovics pedig néprajzi és nyelvészeti kutatásokat folytatott. Ez utóbbira Hell kérte fel, aki egy Daans nevű lapp emberrel történt beszélgetés során vette észre a magyar és a lapp nyelv rokon vonásait (Kelemen, 1978).

8. ábra.Ismeretlen bécsi szerző rézmetszete.
Készült az Arteria Műkiadónál. Aláírása a következő: „R. P. Maximilianus Hell e S.J. Astyronomus Regio-Caesareus, observato feliciter Transitu Veneris ante Discum solis die 3º Junii 1769 Wardoehusii in Lapponia Finnmarchica, Votis Christiani VII Danie et Norvegiae Regis impletis, in Veste sua Lapponica (1771)”, azaz Hell Miksa tisztelendő úr, a Jézus-Társaság tagja, császári-királyi csillagásza, aki szerencsésen megfigyelte 1769. június 3-án a finnországi lappföldi Wardöhusban [Vardö szigetén] a Venus-bolygónak a Nap korongja előtt való átvonulását VII. Keresztély, Dánia és Norvégia királyának engedélyével, Lappföldön használt öltözetben (Herman, 1891, Heindrich, 1978).
A rézmetszet előkerülését Hermann Ottónak köszönhetjük, aki 1891-ben Hell után kutatva, a véletlen által segítve talált rá Hell rokonainál. Hermann cikkében fölhívja a figyelmet, hogy a „jó páter” lapp öltözéke alól „kikandikál az attila” (Hermann, 1891).
A rézmetszet levonatának egy példányát a XX. század közepéig a kolozsvári Báthory Líceum fizikumának szertárában őrizték. Sajnos mára már nyoma veszett.
Hell a számítások elvégzése után a Nap parallaxisára 8,7 ívmásodpercet kapott, amely nagyon közel áll a ma elfogadott 8,79 ívmásodperces értékhez. Munkájáról először VII. Keresztély királynak számolt be, ezért kis késedelemmel tette közzé eredményeit (Hell, 1770). Közben Lalande híres francia csillagász türelmetlenségében kétségbevonta a kapott megfigyelési adatokat. Hell válaszára azonban elismerte az adatok helyességét, és nyilvánosan bocsánatot kért. Az eredmények hitelességét később Hell utódja a bécsi csillagda igazgatói székében, K. L. LITTROW is megkérdőjelezi, egészen az észlelések meghamisításával vádolva Hellt. Ezeket a támadásokat csupán 1883-ban utasítja vissza Simon NEWCOMB neves amerikai csillagász, a parallaxis kérdés jeles szakértője, aki bebizonyítja Littrow tévedését és Hell eredményeit tisztelettel méltatja (Bartha, 1969; Ley, 1968).


9. ábra. Az 1769. június 3-i Vénusz-átvonulás Vardö-i megfigyelésére vonatkozó adatokat közzétevő Hell-publikáció címlapja és az észlelési adatok.
Két esztendeig és három hónapig tartó távollét után Hell és Sajnovics 1770. augusztus 22-én érkezik vissza Bécsbe, ahol tovább folytatja munkáját, amelyet a jezsuita rend eltörlése (1773) sem gátol meg. Tovább szerkeszti az évkönyveket és gyűjti a csillagászati megfigyeléseket. Szerette volna felállítani a Tudományos Akadémiáját, de erre éppen a rend eltörlése miatt már nem került sor (Kölesy–Melczer, 1816).
Amidőn II. József császár uralkodása alatt eltörölték a jezsuita rendet, Hell Miksát Londonba hívták, ahol fontos és előkelő tudományos állást ajánlottak fel neki. Ha a londoni meghívást elfogadja, akkor ismét névváltoztatásra kellett volna gondolnia, mivel az angol hell szó szintén poklot jelent, mint a német Höll, amely jelentés korábban nevének megváltoztatását okozta (Heinrich, 1978).


10. ábra. Hell által javasolt csillagképeket tartalmazó térkép és egy oldal Hell kézírásával.
Hell tudományos érdeklődése igen széleskörű volt. Csillagászati és matematikai munkássága mellett foglalkozott fizikával, geodéziával, térkép és földgömbkészítéssel, éghajlattannal, nyelvészettel, történelmi kutatásokkal és még sok mással. Érdekességként megemlíthető, hogy a magyar történeti földrajz tudományának is egyik megalapozója, ugyanis Hell ábrázolta elsőként térképen Anonymus földrajzi adatait, szöveges magyarázót is tervezve és (részben) készítve is művéhez. Hell kéziratos Anonymus-térképei 1771-72-es jelzetet viselnek. Nyomtatásban 1801-ben jelent meg, a térképet metszette: Prixner Godofred (Tóth, 2005).
Hell Miksa 1792. április 14-én halt meg Bécsben lázas hurutos megbetegedésben (tüdőgyulladásban), amelyet akkor szerzett, amikor a Bécsbe látogató török követség tagjainak betegen és erősen rekedten minden kérdésére készségesen felelt (Kölesy–Melczer, 1816). Egyik barátja, B. Benkler Nyugat-Lichtensteinban emlékoszlopot állított nevének megörökítésére. (Feliratát a Magyar Kurir is közölte 1792-ben.) Ezen Dénes udvari tanácsos és könyvtáros alábbi verssorai voltak olvashatók:
„Corpore dum posito levior tellure relicta,
Candidus ad Superos Hellius urget iter,
Et nunc Stellas, nunc illas, transvolat inquit:
Sat vos suspexi, despicere incipiam.”
(Prózai magyar fordításban: „Megszabadulva a testtől és a hátrahagyott földnél könnyebben, a kiváló Hell az égitestek felé veszi útját, és most ezeket, majd amazokat a csillagokat repüli át, és így szól: eleget vizsgáltalak titeket alulról, most felülről kezdelek nézni benneteket.”) (Heinrich, 1978) Hell tudományos munkásságát az európai akadémiák is siettek elismerni: rendre tagjává választotta a párizsi, bolognai, koppenhágai, stockholmi, göttingai, trondheimi tudós társaság (Döbrentei, 1817).
Az utókor elismerését tükrözi egy nevét viselő Hold-kráter és a halálának kétszázadik évfordulója alkalmából kiadott bélyeg is, amely Hell képmását őrzi.
{mosimage}
Hell Miksa fontosabb, nyomtatásban megjelent publikációi
1745 Elementa Algebrae Joannis Crivelli magis illustrata et novis demonstrationibus et problematibus aucta. név nélkül. (Crivelli könyvének Hell által fordított, bővített és javított kiadása.)
HÖLL, Maximilianus
1755a Elementa mathematica naturali philosophiae ancillantia. Tomus I: Elementa Arithmeticae numericae, et literalis seu Algebrae. Claudiopolitanae, 1755.
1755b Exercitationum Mathematicarum. Pars I. Exercitationes Arithmeticae/em>, Claudiopolitanae.
1755c Materia Tentaminis Mathematici.Aula Academica S. J. Claudiopolitanae, die 14. Mensis Julii.
HELL, Maximilian
1762 Anleitung zum nutzlichen Gebrauch der künstlichen Stal-Magneten. Wien.
1770 Observatio transitus Veneris ante discum Solis, die 3 Junii Anno 1769. Wardoëhusii. Hafniae,.
Bibliográfia
- ANDONIE, George Şt.: Istoria ştiinţelor în România, Matematica, Mecanica, Astronomia, Editura Academiei R.S.R., Bucureşti, 1981.
- Ifj. BARTHA Lajos: Hell Miksa expedíciója és a csillagászati egység kérdése. Csillagászati évkönyv. Budapest,1969, 146–164. old.
- Ifj. BARTHA Lajos: Magyarok a Sarkkörön túl. Hell Miksa és Sajnovics János vardǿi expedíciójának 200. évfordulójára.Élet és Tudomány, 1969, 1208–1212. old.
- CAVALLONI Ferenc: Hell Miksa, a magyar jezsuita csillagász. Katholikus szemle. LIII. Évf. 1939. I. Köt. 31–36. old.
- CSABA György Gábor: A csillagász Hell Miksa írásaiból, Magyar Csillagászati egyesület, Budapest, 1997.
- DEZSŐ Loránt: A magyar csillagászat története. Múzeumi füzetek, Kolozsvár, 1944. 2. évf. 1. szám.
- DÖBRENTEI Gábor: Hell Maximilián élete. Erdélyi Múzeum. 1817. VIII. 88–95.
- ENDREY Elemér: Magyar csillagászok a XVIII. Században. Természettudományi közlöny. 1911. XLIII. Köt. 651–652. old.
- HEINRICH László: Az első kolozsvári csillagda, Kriterion Könyvkiadó, Bukarest, 1978.
- HEINRICH László: Hell Miksa (Maximilian Höll) kolozsvári tevékenysége. Természet Világa 119. 1988.
- HERMAN Ottó: Hell Miksáról. Pótfüzetek a Természettudományi Közlönyhöz. 1891. 2. sz. 51–64. old.
- HŐKE Lajos: Hell, Sajnovics és a magyar jezsuiták. Atheneum. I. évf. 23. sz. 1472–1475. old.
- LEY, Willy: Observatorii cerului, o istorie neobişnuită a astronomiei de la babilon până la era cosmică, Editura Tineretului, 1968.
- KELEMEN János: A magyar csillagászat rövid története. in Whitney, Charles Allen: A Tejútrendszer felfedezése. Ford.: Kelemen János. Gondolat Kiadó, Budapest, 1978, pp. 243-259.
- KÖLESEY Vincze Károly – MELCZER Jakab: Hell. Nemzeti Plutarkus, Pest, 1816. III. Köt. 124–132. old.
- KULIN György – RÓKA Gedeon: A távcső világa, Gondolat Kiadó, Budapest, 1980.
- MARIAN, Victor: Maximilian Hell (Höll) şi activitatea sa la Cluj. Gazeta Matematică 49 (1943/44) , 63–72.
- PAPP Márton: Hell Miksa. Természettudományi Közlöny. 1869, 343–348 old.
- PINZGER Ferenc: Hell Miksa emlékezete. Budapest 1920 (I. rész) és 1927 (II. rész).
- SZENKOVITS Ferenc: Maximilian Hell la Cluj, Lucrările Seminarului Didactica Matematicii, vol. 18 (2001), pp. 159–162.
- B. SZABÓ Emese: Hell Miksa emlékezete. Föld és Ég. 1970. V. évf. 3. sz. 74. old.
- TÓTH Álmos: A hazai történeti földrajz gyökerei. (kézirat), 2005, (http://csillagaszattortenet.csillagaszat.hu).
- ZETÉNYI Endre: Hell Miksa csillagász. Eger, 1970.
Maximilian Hell (1720–1792)
Astronomer Maximilian Hell (initially Höll) was born at Schemnitz in Hungary, 15 May, 1720; died at Vienna, 14 April, 1792. He entered the Society of Jesus at Trentschin, 18 October, 1738, and after his novitiate was sent to Vienna, where he made his philosophical studies. From his early years he had shown a strong inclination for scientific pursuits, and in 1744 he devoted himself to the study of mathematics and astronomy, acting at the same time as assistant to Joseph Franz, the director of the observatory at Vienna. After teaching with much success for a year at Leutschau, he returned to Vienna to study theology, and in 1751 was ordained priest. He received a professorship of mathematics at Klausenberg in 1752, and remained there until 1755, when he was appointed director of the imperial observatory at Vienna.
Hell’s most important work was perhaps the annual publication of the "Ephemerides astronomicæ ad meridianem Vindobonensem", which he began in 1757 and continued for many years. These contain a large number of valuable observations and data. He was invited by the King of Denmark to undertake at Vardöhuus, Norway, the observations of the transit of Venus of 1769. The transit observations were successful, and after spending some months in Copenhagen preparing his results for the press, he returned to Vienna in 1770. Owing to delays in publication Hell was afterwards suspected of manipulating his data to make them fit with others taken elsewhere. The suspicion was strengthened by Littrow when director of the Vienna Observatory, after a study of the original manuscripts (cf. Hell’s "Reise nach Wardö u. seine Beobachtung des Venus-Durchgangs in Jahre 1769", Vienna, 1835). It was not until 1890 that Father Hell’s reputation was cleared of the stain of forgery by Professor Simon Newcomb, who made a critical study of the journal in question, and showed conclusively that Littrow’s inferences were entirely at fault. The latter, it appears, had originally been led into error by a defect in his sense of color. Father Hell was of a gentle disposition and simple in his tastes. His devotion to the Church and to his order often cost him much persecution. Besides his "Ephemerides", he was also the author of "Elementa algebræ Joannis Crivelli magis illustrata" (Vienna, 1745); "Adjumentum memoriæ manuale chronologico-genealogico-historicum" (Vienna, 1750); "Elementa mathematica naturali philosophiae ancillantia. Tomus I: Elementa Arithmeticae numericae, et literalis seu Algebrae " (Claudiopolitanae, 1755); "Exercitationum Mathematicarum. Pars I. Exercitationes Arithmeticae" (Claudiopolitanae, 1755); "De la célébration de la Pâque" (ibid, 1761); "De satellite Veneris" (ibid, 1765); "De Transitu Veneris" (Copenhagen, 1770), etc.
A Technical Review, Historia Scientiarum 2005. évi 30. számában megjelent cikk másodközlése











