A kérdésre egyáltalán nem egyszerű a válasz. Amikor már az egész belátott Univerzummal összemérhető távolságokról esik szó, egyáltalán nem mindegy, hogy:
- hogyan definiáljuk egy adott égitest távolságát
- mit tételezünk fel az Univerzum szerkezetéről.
A technikai részleteket mellőzve adunk ízelítőt a probléma bonyolultságáról. A matematikai szempontból egyik legkönnyebben kezelhető (de azért még realisztikus) kozmológiai modell az ún. Einstein–de Sitter-univerzum, amely sík, örökké táguló Világegyetemet ír le, sűrűsége pedig éppen a kritikus határérték a nyílt és a zárt, önmagába visszahulló univerzum sűrűsége között. Ezzel a feltevéssel élve öt fő távolságdefiníció és konkrét távolság-vöröseltolódás kapcsolat írható le.
1. "Sajáttávolság" (proper distance)
Nem mérhető, de valójában ez áll legközelebb a hétköznapi távolságfogalomhoz. Miközben egy távoli galaxis által kibocsátott foton halad felénk, minden egyes kis időintervallumban megtesz egy adott távolságot, ami a kozmológiai tágulás következtében egyre nagyobbá válik. A megfigyelő detektorába való becsapódásig felösszegezhetjük a kicsiny távolságelemeket, hogy megkapjuk, mekkora utat tett meg a foton utazása közben. Ennek vöröseltolódástól való függését az Einstein–de Sitter-univerzumban az alábbi képlet adja meg:
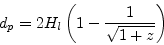
ahol Hl a Hubble-hossz, értéke c/H, azaz a fénysebesség osztva a Hubble-állandóval – utóbbi jelenleg megfigyelhető értéke (72 ± 3 km/s/Mpc) alapján a Hubble-hossz kb. 13,5 milliárd fényév.
2. Luminozitástávolság
Legtöbb csillagászati mérés ezt a távolságot adja. Feltételezve egy égitest abszolút fényességét (M), megmérve a látszó fényességét (m), az m–M=–5+5 log dl távolságmodulusban a dl luminozitástávolság szerepel. Alapja az a feltevés, hogy egy L luminozitású égitest által kibocsátott sugárzás a távolság négyzetével fordítottan arányosan csökkenő fluxussűrűséggel észlelhető. Ennek z-függését az alábbi képlet adja meg:
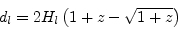
ahol a jelölések a fentiekkel azonosak. Kis vöröseltolódásokra a közelítő képlet:
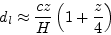
ami mutatja, hogy 0,4-es vöröseltolódásnál az egyszerű lineáris Hubble-törvénytől már 10%-os eltérést tapasztalunk, azaz nem elhanyagolhatók a kozmológiai hatások.
3. Látszószögátmérő-távolság
Ismert átmérőjű objektum látószögéből egyértelműen kiszámítható a távolsága. Végigzongorázva a Világegyetem geometriájára vonatkozó összefüggéseket, kiderül, hogy egy objektum valódi átmérőjéből és a megfigyelt szögátmérőjéből származtatott távolsága másképpen függ a vöröseltolódástól, mint az előbbi két változat:
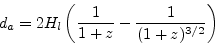
Ezen összefüggésnek van egy meglepő tulajdonsága: z=1,25 körüli vöröseltolódásnál minimuma van, azaz az ennél nagyobb vöröseltolódásokra az egyre távolabbi objektumok nem egyre kisebbeknek, hanem egyre nagyobbaknak látszanak – legalább is egy Einstein–de Sitter- univerzumban! Mindezt fizikailag úgy is lehet értelmezni, hogy ekkora távolságok mellett az egész Univerzum mint egy hatalmas gravitációs lencse felnagyítja a legtávolabbi égitestek képét.
Az effektus kimutatására voltak kísérletek, de a fő probléma, hogy nincs standard kozmológiai méterrúdunk, aminek ismerjük a valódi méretét különböző távolságokban, így egyértelmű megfigyelési eredményekről nem lehet beszámolni.
4. Sajátmozgás-távolság
Ha valahonnan ismernénk egy távoli objektum látóirányra merőleges sebességét és megmérnénk az égi pozícióváltozásként értelmezett sajátmozgását, a kettő aránya egy újabb távolságdefiníciót tesz lehetővé. Ennek z-től függését a
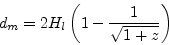
összefüggés adja meg, ami az elsőként megadott sajáttávolsággal megegyezik.
5. Visszatekintési időből származó távolság
A legközelebbi csillagról a fény 4 év alatt ér ide, azaz mondhatjuk azt, hogy távolsága 4 fényév. Hasonlóan, kiszámíthatjuk, hogy egy z vöröseltolódású galaxisból kibocsátott fény mennyi ideig utazott, ami a fényidőtávolság, vagy visszatekintési időből származó távolság definiálását teszi lehetővé. Ennek z-től függése

alakú.
Kis vöröseltolódásokra természetesen az öt távolságdefiníció értéke jó közelítéssel megegyezik. z=2 körül viszont már nagyon jelentős az eltérés: legkisebb a da szögátmérőtávolság, kb. 0,3 Hl, majd következik a dt fényidőtávolság 0,55 Hl értéknél. dp és dm megegyezik, kb. 0,85 Hl, a legnagyobb pedig a dl luminozitástávolság, több mint 2,5 Hl értékkel.
Gyakorlatban dt jól visszaadja a fizikai intuíciónk által értett távolságot, dl pedig a csillagászati mérésekből számított távolságot. De mint a példa mutatja, még ezek között is közel hármas szorzóbeli eltérés tapasztalható. Bonyolultabb kozmológiai modellekben természetesen a fenti távolság-vöröseltolódás kapcsolatok is bonyolultabbak lesznek, de ezek részletezése már túlmutat a válasz keretein.
Felhasznált irodalom: S. Webb, 1999, Measuring the Universe – The Cosmological Distance Ladder, Springer-Praxis











