A ptolemaioszi földrajzi hosszúságok azonban terhes örökségnek bizonyultak. A bajt az okozta, hogy a Föld sugarát az ókorban a valóságosnál kisebbnek tudták. A távolsági adatokra alapozott térképezések így azt eredményezték, hogy az ismereteik szerinti lakott föld terjedelme jól kitöltötte a földglóbusz felületét. Európa nyugati partvonala és Japán (Cingapu) között alig maradt 90°-nyi – nyílt tengernek tudott – gömbfelület. Ki gondolta volna, hogy oda még egy kontinens beékelődik? A sors iróniája, hogy a ptolemaioszi Geográfia-kiadások éppen a nagy földrajzi felfedezések időszakában élték virágkorukat. Kolumbusz nem is sejtette, hogy a ptolemaioszi földrajzi hosszúságok mennyire megtréfálták. A nagy tévedésre csak az utána következők jöttek rá.
MISSING DST IMAGE!!!!
1. ábra.
A földrajzi helymeghatározás technológiáját tudományos alapokra kellett helyezni. A figyelem az ez idő tájt feltűnt rugós felhúzású, hordozható kerekes órákra terelődött. Ha a kiinduló állomás helyi ideje szerint jártak, időegyeztetés útján elvileg alkalmasak lettek volna λ-különbségek meghatározására, csakhogy egyenetlen járásuk, meg egyetlen mutatójuk kizárta gyakorlati alkalmazásukat.
Antonio Pigafetta (1491-1534), Magellán munkatársa és Johannes Werner (1468-1528) közel egyidőben jött rá, hogy a Holdnak az állócsillagok közti helyzetváltozása felhasználható a földrajzi hosszúságkülönbség meghatározására. Ezt a – szintén időegyeztetésen alapuló – módszert Petrus Apianus (1495-1552) és Gemma Frisius (1508-1555) is ismertette.
Hasonló eljárást írt le hazánk fia, Pühler Kristóf, az 1563-ban Dillingenben kinyomtatott Eine kurtze und grundliche Anlaytung zu dem rechten verstand Geometriae című kézikönyvében1. Pühler előbb gyakorlati földmérési eseteket, majd csillagászati alapfogalmakat tárgyal. A 60. fejezetben (1. ábra) tér át a földrajzi hosszúságkülönbség problémájára. A megoldás nyitja nála is az, hogy a Hold az égbolton nem mozog együtt az állócsillagokkal, hanem közöttük mintegy előresiet, és így napi rektaszcenziója a naptári nap függvényében 11°-15°-kal nő.
Mármost, ha eltérő földrajzi hosszúságú két észlelési ponton ugyanaznap a Holdnak a helyi meridiánra érkeztekor (kulmináció) mérjük a Hold-állócsillag egyenlítőre redukált szögtávolságát, a szögkülönbség arányos lesz az álláspontok földrajzi hosszúságkülönbségével. Egy, a kiindulási helyre előre kimunkált almanach birtokában az aktuális szögtávmérést csak a meghatározni kívánt ponton kell elvégezni.
MISSING DST IMAGE!!!!
2. ábra.
A leírtakat a könyv a 2. ábrán szemléltetett példával teszi érthetőbé. 1557. október 10-én a meghatározni kívánt állásponton (v) holdkulminációkor az alfa Orionis (s) és a Hold (1) között 6°50′ egyenlítőre redukált szögtávolságot (fd) mértek. Az almanach szerint ugyanaznap a kiindulóállomáson, Passauban (z) ez az érték gd = 9°45′. A két szögérték különbsége gh = 2°55′ úgy aránylik a Hold rektaszcenziójának aznap 24 óra alatti növekedéséhez (az almanach szerint 1557. október 10-én 15°22′), mint Passau és az észlelési hely (v) közti földrajzi hosszúságkülönbség (Δ λ) aránylik a 360°57′-hez, ahol 57′ a Nap rektaszcenziójának aznapi növekedése. Tehát 2°55′ : 15°22’= Δ λ: 360°57′. Ebből Δ λ=68°35′. Mivel a 6° 50′ kisebb, mint a Passaura vonatkozó 9°45′, az észlelési hely Passautól nyugatra fekszik.
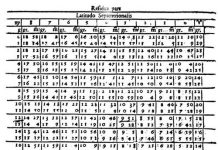
Pühler könyvében közöl egy – az eljárás gyakorlati alkalmazására szolgáló – az 1560. esztendőre kimunkált, 22 fényes csillagot tartalmazó táblázatot (3. ábra). Úgy válogatott össze +16 és -10 fok közti deklinációjú csillagokat, hogy rektaszcenziójuk szerint egyenletesen elosztva, az év bármely szakában Közép-Európában valamelyikük észlelhető legyen.
A mérés kivitelezésére Pühler különleges műszert2 tár elénk. Alkatrészenként részletesen leírja, és rajzban illusztrálja. Formája kakastaréjra emlékeztet, innen a neve: gallus (= kakas; 4. ábra). Bármennyire eltérő is a külseje, felépítésének elve mégis azonos a Ptolemaiosz-rendszerű egyenlítő-gyűrűs asztrolábiuméval, csupán a gyűrűknek az észlelés során nem használt szektorait kiiktatták az alábbiak szerint:
– Az egyenlítő-gyűrűnek (a) csupán 66°-nyi ívét hagyták meg.
– A meridiángyűrűt (b) kvadránssal helyettesítették.
– A deklinációs gyűrű (c) megfelelő szektorát +30° és -30° közötti deklinációk mérésére korlátozva, szárnylapon alakították ki.
A szögtávmérés végrehajtása a gallusszal
A szárnylapot a forgókarral összecsukva, a taréj (kvadráns) síkját beállítom álláspontom meridiánjának síkjába. Ezt követően a taréjt közrefogó forgókar ablakvágatának indexül kialakított leolvasó élét ráállítom a taréjon az álláspont földrajzi szélességének pótszögére (90° – φ). Ezáltal a műszer egyenlítő-íve párhuzamossá vált az egyenlítő síkjával. A szárnyak eme összecsukott állapotában várom, hogy a Hold a taréj síkjába érjen (kulmináljon). Megkönnyítendő a dolgomat, az irányzóvonalzó (alhidade) ablakvágatának irányélét már előre ráállítottam a Hold aznapi deklinációjának az almanachból kiolvasott értékére, mert így a Hold az irányzólyukacskák, ill. az irány irányzócső irányvonalába. Bekövetkezvén a holdkulmináció, a szükséges mértékig szétnyitott szárnyállásban megirányzom a kiszemelt állócsillagot. Az egyenlítő-íven a taréj síkja máris kimetszette a csillagnak a helyi meridiántól mért szögtávolságát.
MISSING DST IMAGE!!!!
3. ábra.
Ez utóbbi mérési fázis is egyszerűsödik, ha az irányzást úgy hajtom végre, hogy előzőleg az alhidade-ablak irányélét a csillag deklináció-értékére állítom rá.
Megoldotta-e a problémát a Hold-állócsillag szögtávmérés módszere?
A műszer a korabeli technika szintjén valósult meg. Konstrukciós fogyatékosságait a finommechanikai megmunkálás nem pótolhatta. Talpcsavarok híján az állótengelyt az aljzat aláékelésével, függő útján tették függőlegessé. Nem lévén még precíziós körosztógép, az osztásvonásokat kézi úton vésték fel. Az 1 fokonkénti körosztáson a leolvasás élességét átlós segédosztás útján sem tudták 10′-nél pontosabbá tenni. A taréj síkját megítélésünk szerint is csak 2-3 ívperc pontossággal tudták a meridián síkjába beállítani. A pontos irányzást finommozgató csavar hiánya nehezítette. A nehézséget az is fokozta, hogy a szabadszemes irányzáskor a szemnek váltakozva kellett alkalmazkodnia az alhidade nézőkéihez és az irányzott égitesthez, mely nem is volt mozdulatlan. Nem elhanyagolható az a körülmény sem, hogy a közel másfél méteres műszernagyság ellenére az egy fekvésben végzett mérést szabályos hibák terhelték, amit nem ellensúlyozott a mérést végző személyek gyakorlata és érzéke. Megítélésünk szerint a gallust méréskor – miként a Ptolemaiosz-rendszerű gyűrűs asztrolábiumot is – két személy szolgálta ki.
A felsoroltakat mérlegelve a szögtávmérés pontosságát 10 ívpercre becsüljük, ami a földrajzi hosszúságkülönbség meghatározásának mintegy 3°-os hibáját vonja maga után. Hazánk földrajzi szélességén ez az érték 230 km-t tesz ki, és ez a korabeli igényeket sem elégítette ki. A problémára megoldást majd csak az 1740-es évek után hoz az angol John Harrison hajózási kronométere.
{mosimage}
4. ábra.
Nem lenne teljes írásunk, ha Pühler Kristófról és könyvéről néhány szót nem ejtenénk. Pühler a történelmi Magyarország területén, a Sopron megyei Siklóson
(ma Sigless) született. Életéről alig tudunk valamit. 1517-ben írták he nevét a bécsi egyetem anyakönyvébe. 1521-ben megkapta a szabad tudományok borostyán
koszorús fokozatát. Egyetemi évei alatt szoros barátság alakult ki közte és tanulótársa, a már említett Petrus Apianus között, aki az 1524-ben kiadott Cosmographicus liber-jében a 11 magyarországi helység földrajzi koordinátái között Siklósét is megadta, azzal a megjegyzéssel, hogy ott született Pühler.
Pühler, belépve az Ágoston-rendbe, a Passau melletti Sankt Nikola kolostorban élt, és a kolostori iskolában tanított. Megfordult a Wolfgang von Salm passaui hercegérsek köré csoportostult humanisták körében is. Könyvének kéziratát 1561-ben fejezte be. Magas kort ért meg, 1583 táján halt meg.
Könyvének öt hazai példányáról tudunk. Az MTA Csillagászati Kutató Intézetében őrzött példányban kéziratos bejegyzés tanúsítja, hogy a könyvet Jonas Adelwert passaui orvos 1567-ben kapta attól a Bartholomaeus Madauer aldersbachi apáttól, akinek Pühler a könyvét ajánlotta.
Megjegyzések:
1. Pühler könyvének kritikai elemzéssel ellátott teljes magyar fordítását a Pécsi Geodéziai és Térképészeti Vállalat 1974-ben 600 példányban megjelentette Pühler geometria practicája címen.
2. A műszer kicsinyített mását 1991-ben Pécsett az V. Országos Csillagászattörténeti Találkozón bemutattuk és használatát ismertettük.
A Meteor 1995/5. számában megjelent cikk internetes változata