A Titius-Bode szabály a csillagászat iránt érdeklődők körében talán az egyik legismertebb matematikai formula. Bár különböző változatai már korábban több szerző munkáiban megjelentek, mai formája leginkább két német, Johann Daniel Titius és Johann Elert Bode megfogalmazásának köszönhető. Előbbi Charles Bonnet 1764-es "Contemplation de la Nature" című munkájának általa készített 1766-os német fordításába csempészte be lábjegyzetként, míg utóbbi 1768-as "Anleitung zur Kenntniss des gestirnten Himmels" című művében említette szintén lábjegyzetként, ekkor még hivatkozás nélkül, a munka későbbi kiadásaiban azonban már Titiust jelölve meg forrásként. A szabály lényege, hogy a formula
0,4 + 0,3 · 2n
alakjában n helyébe a -∞, 0, 1, 2, … értékeket írva rendre a Naprendszer nagybolygóinak a félnagytengelyeit kapjuk. A képlet jól adta vissza az értékeket az összes akkor ismert bolygóra, sőt még az 1781-ben felfedezett Uránusz is beleillett a sorba. Zavaró momentumként csak az jelentkezett, hogy az n = 3 értékhez tartozó a távolságnál nem volt bolygó. Ez a hiány ugyanakkor kétségtelenül inspiráló hatással is bírt, s a szabálynak minden kétséget kizáróan fontos szerepe volt először a Ceres, majd a Pallas, a Juno és a Vesta kisbolygók felfedezésében is.
A formulával azonban akadtak gondok is. Az első, hogy a Merkúr esetében szükséges -∞ a kitevőben "nem szép", s mindenképpen nehezen magyarázható, ha a szabály esetleges fizikai hátterét kutatjuk. Ennél azonban valószínűleg nagyobb csapást jelentett rá a Neptunusz 1846-os felfedezése, mert pályájának félnagytengelyére teljesen rossz eredményt adott. Természetesen már a kezdeti időktől fogva foglalkoztatja a kutatókat az, hogy az eredeti "szabály", illetve modernebb megfogalmazásai mögött áll-e valamilyen fizikai ok, vagy csak véletlenül alakultak így a pályaviszonyok a Naprendszerben. A legújabb elképzelések alapján úgy tűnik, hogy bolygórendszerünk mai konfigurációja egy dinamikai fejlődés eredménye, a Titius-Bode szabály pedig nem eleve bekódolt, hanem ezen fejlődés során szerzett tulajdonsága. (A bolygórendszerek, ezen belül a Naprendszer keletkezésével kapcsolatos modern elméletekről Petrovay Kristóf összefoglaló cikkében olvashatunk bővebben a 2008-as Csillagászati Évkönyvben.)

Fantáziarajz az 55 Cancri Neptunuszhoz hasonló méretű bolygójáról.
[University of Texas, NSF, NASA]
Az elmúlt másfél évtized kutatási eredményeinek köszönhetően ma már nem csak a Nap, hanem más csillagok planétáiról is rendelkezünk ismeretekkel. A mai napig a NASA JPL Planetquest oldala szerint 238 csillag 277 bolygóját azonosították. A két szám azt jelenti, hogy vannak olyan csillagok, melyek körül egynél több kísérő kering. A legtöbb bolygóval, szám szerint öttel az 55 Cancri csillag rendelkezik, az ötödik felfedezését 2007 őszén jelentették be.
Arcadio Poveda (Instituto de Astronomía, Universidad de México) és Patricia Lara (Facultad de Ciencias, Universidad de México) úgy gondolták, hogy öt bolygó már elegendő ahhoz, hogy becsült pályaelemeik ismeretében megvizsgálják, vajon a Titius-Bode szabályhoz hasonló formula működik-e más bolygórendszerekben is. Ehhez először kicsit átalakították a tradicionális formulát, s egy exponenciális illesztést alkalmaztak, azonban a Naprendszer esetében kihagyták a Merkúrt a már korábban említett ok miatt, de kimaradt a Pluto is a nagybolygókhoz képesti extrém pályaelemei, illetve "tisztázatlan" státusza miatt. Figyelembe vették viszont az Uránuszt és a Neptunuszt is. Az illesztés eredménye a
a = 0,1912 e0,5594n
formula, ahol n = 2 a Vénusznak, míg n = 9 a Neptunusznak felel meg, de n = 1 esetben a Merkúrra is viszonylag jó eredményt ad. Érdekes, hogy a klasszikus formulával ellentétben ebből az illesztésből nem a Neptunusz, hanem az Uránusz lóg ki jobban.
Poveda és Lara hasonló exponenciális illesztést végeztek el az 55 Cancri öt bolygójára is, eredményül az
a = 0,0148 e0,9781n
formulát kapták. A numerikus munka során azonban azt tapasztalták, hogy ha az ötödik bolygóhoz az n = 5 értéket rendelik, akkor a távolságértéke rendre messze esik a másik négy bolygó félnagytengelyeire illeszkedő bármely elfogadható exponenciális görbétől. Ha azonban az n = 6 értéket rendelik hozzá, akkor nagyon jó illeszkedést kapnak.
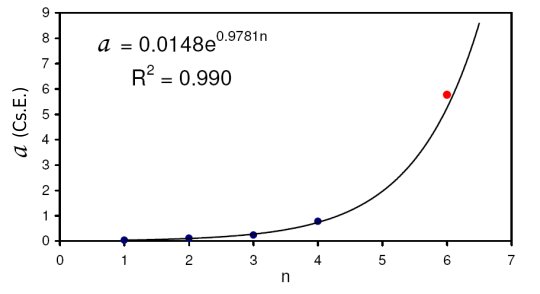
Az 55 Cancri rendszer négy belső bolygójának távolságértékeire (kék pontok) illeszkedő exponenciális görbe, melyhez az n = 6 választással nagyon közel van az ötödik bolygó félnagytengelyének értéke is (piros pont).
[Poveda és Lara]
Ez azonban azt jelentheti, hogy az 55 Cancri esetében hasonló helyzettel állhatunk szemben, mint két évszázaddal ezelőtt a Mars és a Jupiter közötti objektum keresésekor! Az ötödik bolygóra n = 6 feltételezésével kapott
a = 0,0142 e0,9975n
görbe R2 korrelációs együtthatója nagyon jó, majdnem 1, ami alátámaszthatja a választás jogosságát. Ez utóbbi formula eddig egyedülálló módon tehát megjósol egy hatodik bolygót az 55 Cancri rendszerében a ≈ 2 Cs.E. félnagytengelyű pályával! A görbe extrapolációjából egy hetedik bolygó esetleges létezése is kiolvasható a ≈ 15 csillagászati egységnél, de ennek valószínűsége már jóval kisebb.
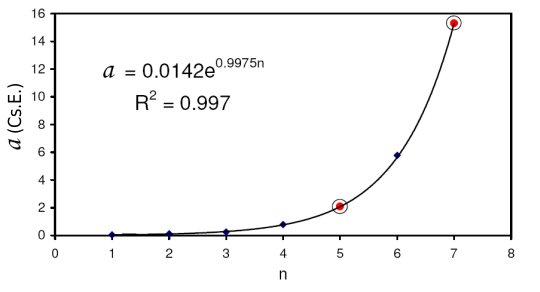
Az 55 Cancri hipotetikus hatodik és hetedik bolygóját piros körök jelzik.
[Poveda és Lara]
A munka nem csak azért figyelemre méltó, mert előrejelzi egy (illetve kettő), eddig még fel nem fedezett bolygó létét egy exobolygó-rendszerben, hanem azért is, mert alátámasztja azt, hogy a Titius-Bode szabály létezése nem a véletlen műve, azaz valamilyen fizikai oknak kell állnia mögötte.
Az eredményeket részletező szakcikk a Revista Mexicana de Astronomía y Astrofísica c. folyóiratban fog megjelenni.
Forrás:
- arXiv:0803.2240v1 [astro-ph]