2009 a Csillagászat Nemzetközi Éve
Az Egyesült Nemzetek Szervezete, Galilei mérföldkőnek tekinthető csillagászati felfedezése tiszteletére, a 2009. évet a Csillagászat Nemzetközi Évévé nyilvánította, amelynek ünnepélyes évadnyitójára január 15-én került sor Párizsban, az UNESCO és a Nemzetközi Csillagászati Unió együttműködésben. A csillagászati évben a Szentszékhez kapcsolódó intézmények is több kezdeményezést indítottak: A firenzei jezsuiták Stensen Intézete Nemzetközi Tudományos Kongresszust szervez „A Galilei-per történeti, filozófiai, teológiai újraértelmezése” címmel, a Kultúra Pápai Tanácsával, a Pápai Tudományos Akadémiával és a Vatikáni Csillagvizsgálóval együttműködésben; a Vatikáni Múzeumban kiállítás nyílik „Astrum 2009: Az olasz csillagászat történelmi öröksége Galileitől napjainkig” címen; a Szentszék tervei között szerepel a Galilei-per teljes anyagának új kiadása is, a Vatikáni Titkos Levéltár gondozásában.2
A Magyar Csillagászati Egyesület, és sok más szakmai szervezet, egyetem, főiskola, szakkör, iskola és múzeum is méltó módon kívánja megünnepelni a Csillagászat Nemzetközi Évét. Fő célkitűzésünk, hogy minél több embert megismertessünk az Univerzum csodáival – előadások, cikkek, kiállítások, távcsöves bemutatók, vetélkedők és egyéb programok formájában.3 Ez a tanszertörténeti írás is ezért, és a természettudományos oktatás érdekében született; de néhány különleges csillagászati taneszköz bemutatásával a TanszerMúzeum sorozathoz is kapcsolódik.

Az Országos Pedagógiai Könyvtár és Múzeum Könyv és Nevelés c. folyóiratának öt esztendeje indult elektronikus változatában, a „Tanszermúzeum” rovat második, kis írása4 volt a „Modellek egyes csillagászati földrajzi fogalmak szemléltetéséhez” címet viselő, illusztrált tanszertörténeti tanulmány. Ebben kísérletet tettem a leggyakrabban használt, muzeális csillagászati eszközök, demonstrációs modellek áttekintésére. A cikkben említett, Joseph Wright of Derby (1737-1794) által taneszközként megfestett orrery készülék5 utódai, az 1800-as évek közepétől jól bevált szemléltető eszközök – a tellurium, lunárium, planetárium, horizontárium – lényegében kicsinyített, nem méretarányos, mechanikusan működő, „kozmikus” modellek, amelyek jelentős részhalmazát képezik a csillagászat gazdag eszköztárának
A „mennyiségtani földrajz” tanításához egykori polgári és felsőbb iskoláink, gimnáziumaink könyv- és szertáraiból nem hiányozhatott a szemléltetési célból kiállított armilláris szféra, a földgömb, az éggömb és a csillagabrosz (csillagtérkép), és a műszerek sem; a szextáns, esetleg kvadráns, az asztrolábium, a bussola (kompasz v. iránytű) s főként nem, a Kepler, vagy Galilei-féle távcső. A csillagos égbolt története azonban egykor a megfigyeléssel, és a csillagképek feltérképezésével kezdődött.
400 éve történt – Galilei távcsöve és Kepler törvényei
Az idei esztendő a 400. évfordulója a modern asztronómia kezdetének, vagyis amikor Galileo Galilei (Pisa, 1564. február 15. – Arcetri, 1642. január 8.) olasz természettudós a csillagok tanulmányozása céljából, elsőként az égre szegezte magaalkotta távcsövét. Érdeme az újszerű alkalmazás, hiszen tudjuk, hogy az első távcsöveket Hollandiában már korábban elkészítették, alighanem tengerészeti célokra. Galilei, a telescopiuma segítségével – felfedezte a Jupiter négy holdját, s rájött arra is, hogy a Tejút csillagokból áll, s a Hold sem tökéletes gömb, mivel a felszínén hegyek és kráterek láthatók. Felfedezéseit 1610-ben publikálta a rézmetszetes rajzokkal illusztrált Sidereus Nuncius (Csillaghírnök) c. művében.


400 évvel ezelőtt történt még az is, hogy Johannes Kepler (Weil der Stadt, 1571. december 27. – Regensburg, 1630. november 15.), Tycho de Brahe dán csillagász asszisztense, a katolikus II. Rudolf császár prágai udvari csillagásza kimutatta, hogy a Mars pályája nem kör, hanem ellipszis, és annak egyik gyújtópontjában van a Nap. Megfigyeléseiből levezette, hogy azonos idők alatt azonos területet súrol a bolygók vezérsugara. A két törvényt az 1609-ben megjelent „Astronomia Nova” című művében közölte. Megfigyelte azt is, hogy a bolygók a Naphoz közelebb járva gyorsabban mozognak, mint távol.6 Keplert, tartományi matematikusként naptárkészítéssel is megbízták. Ennek során kiállt a XIII. Gergely pápa által 1582-ben véghezvitt naptárreform mellett.
Galilei és Kepler felfedezéseit ma már a földrajzi tankönyvek és atlaszok, fizika tankönyvek önálló fejezetei tárgyalják, hagyományos és digitális szemléltető és kísérleti eszközök segítségével azokat, bárki megértheti. Kepler legnagyobb művében, a „Mysterium cosmographicum”-ban, azonban a következő önvallomást olvashatjuk: „Három dolgot kutattam főképpen: a bolygópályák számát, nagyságát és mozgását. Arra, hogy ehhez hozzákezdeni merészeljek, a nyugvásban lévő dolgoknak, a Napnak, az állócsillagoknak és a közbeeső térnek, Istennek az Atyával és a Szentlélekkel való szép harmóniája bírt rá.”


240 éve történt – Hell Miksa megfigyelései és az egri Specula
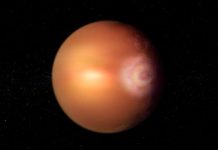
Jelentős magyar évforduló 2009-ben, amely igazán kötődhet a Csillagászat Nemzetközi Évéhez, a Hell Miksa-féle, 1769. évi Vénusz megfigyelés. Az 1760-as években VII. Keresztély, dán és norvég király, Mária Teréziától kért csillagászt a Vénusz bolygó Nap előtti átvonulásának megfigyelésére, amelyet 1769-re vártak. A királynő a feladatra Hell Miksa7 (Selmecbánya, 1720. máj. 15. – Bécs, Ausztria, 1792. ápr. 14.) magyar tudós, jezsuita szerzetest ajánlotta. 240 éve annak tehát, hogy a lappföldi Vardö szigetén Hell, a legismertebb magyar csillagász, a bécsi Egyetemi Csillagvizsgáló első igazgatója, észlelte a Vénusz-átvonulást.8 Útjára elkísérte Sajnovics János (Tordas, 1733. máj. 12. – Buda, 1785. máj. 4.) rendtársa is, aki múlhatatlan érdemeket szerzett a magyar-lapp nyelvrokonság kimutatásával, melyet a természettudományos munka szüneteiben végzett, általában mostoha körülmények között. Hell páter nemcsak az átvonulást figyelte meg, hanem a földrajzi szélesség meghatározására kifejlesztett módszerét is tesztelte, jó eredménnyel. Mérései rendkívül pontosak voltak, az általa meghatározott Föld-Nap távolság hibája 1% alatti. Hell kiváló felkészültségét bizonyítja, hogy a korabeli magyar csillagászati obszervatóriumok tervezésében, műszerezésében és személyzetének kiképzésében is részt vett.
Talán ismeretes, hogy gróf Esterházy Károly 1762-ben kezdte meg püspöki tevékenységét Egerben. Neki, és Hell Miksának köszönhetően még egy nevezetes magyar esemény évfordulója esik biztosan a Csillagászat Nemzetközi Évére. 240 éve már annak is, hogy végleg elkészült a barokk stílusban egyetem céljára épített egri Lyceum, s annak 59 méter magasságú, forgatható kupolájú csillagászati nézőtornya, a „Specula”. A püspök a tervezett négy fakultásból (jogtudomány, teológia, orvosképzés és természettudományok) álló universitas felépítésére, 1764-ben kötött szerződést Fellner Jakab (Nikolsburg, 1722. július 25. – Tata, 1780. december 12.) építésszel, a késő barokk talán legkiválóbb magyarországi mesterével. A csillagvizsgáló torony belső kialakításához Fellner – Esterházy kívánságára – Hell Miksa és Madarassy János9 (Apátfalva [Csanád megye], 1741. augusztus 28. – Eger, 1814.) csillagászok véleményét is kikérte.

A Speculáról 1781-ben a Magyar Hírmondó ezt írta: „Egerbenn a ’Nézőtorony már egészen elkészült. A ’Császári Királyi Udvari Astronomusnak, Főtisztelendő Hell Úrnak hiteles mondása szerént ennél különb Néző Tornyot nem igen látni Európábann. Mellyelis mostani Püspök Úr ő Exellentiája Esterházy Károly Gróf Úr nevezetes Ditsőséget szerzett soha el nem enyészendő hirének-nevének. A’hozzá való eszközök, mellyek messzünnen öszveszereztettek, 15 ezer Forintoknál fellyebb betsültetnek. Mostani Gondviselője… ama nagy hírű nevezetű Hell Úrnak tanitványa. E’ szerént magyar Ország most három nevezetes Néző Tornyokkal ditsekedhetik: az első idejére nézve a Nagy Szombati, a második a Budai, a harmadik az Egri. Ritka az az ország, a mellyben ennyi találkozzék.”

A csillagászati torony a líceum épületének szerves részeként oktatási és kutatási célokat egyaránt hivatott volt szolgálni. Felszerelése is ennek megfelelő.10 „A csillagászati műszereket Hell részint Bécsből, részint pedig Londonból rendelte meg. Egy 1776-ból származó kimutatás szerint Londonból a következő műszereket rendelték meg: négylábas mozgatható kvadráns, két Dollond-féle messzelátóval; az „instrumentum parallacticum” két forgatható meridiánműszer, szintén Dollond-féle tubussal; két csillagászati óra kompenzált ingával; két akromatikus Dollond-féle messzelátó (10 és 15 lábas); ötlábas Newton-féle tubus; ötlábas Heart-féle tubus; két mikroszkóp. A Bécsből megrendelt műszerek pedig a következők voltak: csillagászati óra Niggl műhelyéből; Newton-rendszerű ötlábas tubus; a linea meridiana fölállítására szolgáló műszer; háromlábas Gregory-rendszerű tubus; Jovilabium; a linea meridionalis kiinduló pontjának köve a zsineget tartó készülékkel; a kéziszerszámok tékája, benne a gnomon és más kisebb segédeszközök; barométer. A legnagyobb műszer, amit ezután rendeltek Londonból a hatalmas „quadrans muralis” volt, amellyel a Londonból rendelt műszerek ára 9114 rajnai forintot tett ki.”
Az egri Hell-féle linea meridionalis – műszer és taneszköz
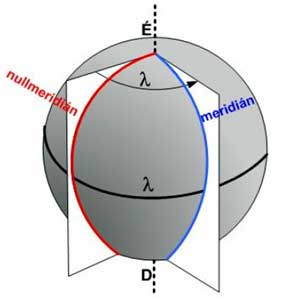
A természetföldrajzi ismeretek között a hosszúsági kör, délkör, a meridián fogalmát, a Föld forgása és a napi, illetve helyi időszámítás közötti összefüggés kapcsán tárgyaljuk. Mindenki tudja, hogy a kezdő meridián11 az angliai Greenwich-en keresztül haladó meridián, de még sok nevezetes délkör van. Dr. Schmidt Ágoston kegyesrendi tanárnak, a Lampel Kiadónál 1900-as „Fizikai és mathematikai földrajz” c. gimnáziumi tankönyvében, pl. a hosszúsági pont még Ferro-tól számíttatik. A nevezetes egri délkör fényképe a Mozaik Kiadó 2001-ben kiadott, HunDidac Aranydíjas „Földrajz 9 – Kozmikus és természetföldrajzi környezetünk” c. tankönyvében is szerepel.

Ezen különleges szemléltető eszköznek, Dr. Zétényi Endre az 1986-os visszaemlékezésében nemcsak értékes történeti, hanem funkcionális leírását is adja: „Az épület K-i oldalán az 1773-1779 között épült 53 m magas „Specula” csillagvizsgáló torony. Ennek hatodik emeletén van a Ny-i észlelőterem, vagy Meridiánterem, melyben a napóraként működő márvány délvonal (Linea Meridionalis) van. A napfény a D-i falon 5 m magasban egy rézlapba fúrt (1778-as évszámot viselő) 5-10 mm-es kis lyukon jut a terembe, melynek öt ablakát zsaluk segítségével besötétíthetik. A terem padlóján horizontálisan épített délvonal É-D irányban átlósan húzódik. A sáv 30,5 cm széles, 15 m hosszú és három hosszanti csíkból áll. A középső carrarai fehér márványból, a szélsők részben tárkányi szürke mészkőből burkoltak.A terem padlójába süllyesztett délvonalat csuklósan behajtható fatáblák védik használaton kívüli időszakban. A helyi dél előtti időszakban a napfény a terembe süt és a padlón 3-4 cm átmérőjű napkép jelenik meg. Ez 3 cm/perc sebességgel vonul K-i irányba és jól megfigyelhető, ahogy metszi a délvonalat. A mérés pontosságát fokozta, hogy a márványsáv felett súllyal kifeszített selyemzsinór húzódott, melynek pontos azimutját12 az É-i falra szerelt csavarral finomítani is lehetett. A napkorong és a zsinór érintkezése igen jól megfigyelhető volt és így a napórai dél idejét 1 másodperces pontossággal meghatározhatták. Ekkor a csillagász felkiáltott a nyolcadik emeleti teraszra, ahol egy diák őrködhetett. Ő húzta meg a DNy-i sarkon csüngő kis harangot és erre a jeladásra várva kondulhattak meg a város templomainak harangjai. Ez 1892-ig a zónaidő hivatalos bevezetéséig így történt a napfényes napokon. Mivel a december-januári hónapokban a Nap alacsonyan delel, a napsugarak a terem É-i falára is felfutottak. Ezért van a délvonalnak egy 1,8 m magas vertikális szakasza is. Ezt barokkos dísszel zárták le. A délvonalat Esterházy Károly egri püspök megrendelésére Hell Miksa csillagász tervezte. 1773-ban az építkezés közben már kijelölte a lyuk kivésésének a helyét, majd 1776. máj. 19-én, személyesen tűzte ki a délvonal pontos helyét. Segítségére Madarassy János volt, az eseményen a püspök is megjelent. .Akkor meghatározták a délvonal földrajzi koordinátáit: 47° 53′ 54” és 20° 23′ 14”. A lyuknapóra két évszázada szolgálja az oktatást és ismeretterjesztést. A termet 1929-ben felújították. 1966-ban csillagászati múzeumot rendeztek be, melyet a nagyközönség is látogathat.”
A „Specula”, ma a Lyceum műemlék épületében működő Eszterházy Károly Főiskola varázstornya és Csillagászati Múzeum.13 A toronyban 2006-ban interaktív természettudományi kísérlet-bemutató Varázsterem14 nyílt, 2008-ban pedig egy csillagvetítős Planetárium.15 A múzeummá vált csillagászati torony 4 új, számítógépes tantermében ma főként médiainformatikát, oktatástechnológiát tanítunk. Jó érzés, hogy köröttünk számos eredeti csillagászati műszer és régi szemléltető taneszköz található; a Camera Obscura-ban működik az 1776-ban létesített, a várost pásztázó periszkóp, és a Hell Miksa udvari csillagász által pontosan kimért nevezetes délvonal.
Az armilláris szféra, mint csillagászati műszer és taneszköz
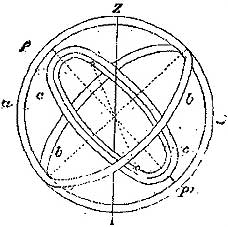
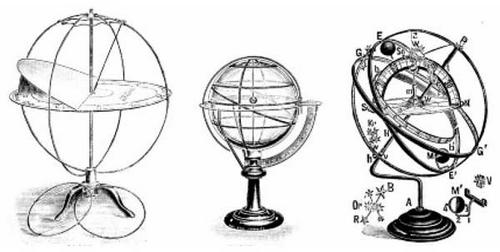
A legtöbb lexikon, így a Pallas nagy lexikona szerint is „az armilláris szféra (lat. s gör.), gyűrűs gömb, elavult csillagászati műszer, az éggömb fontosabb köreit ábrázoló gyűrűkből összetett gömb, mely az égi glóbusszal lényegileg azonos, A régiek a csillagok hosszúságának és szélességének, későbben az óra szögnek és deklinációnak meghatározására alkalmazták. Az a és b kör átegymásra merőleges szilárd összeköttetésű gyűrű, míg c gyűrű a b síkjára merőleges PP1 tengely körül forog. Hozzuk az a síkját a meridiánba, p. azáltal, hogy a delelő Nap felé fordítsuk s alkalmazzunk az a és b metszési ponttól felfelé számított, a geográfiai szélességgel egyenlő ívvel elálló pontban függő ónt: ha ez a gömb középpontján megy át, akkor b az equátor síkjában áll és c valamely deklinációs kört ábrázol. Utóbbi körben más dioptrákkal ellátott gyűrű súrlódással mozgatható; ha egyrészt c forgásával, másrészt a dioptrás kör emelésével vagy süllyesztésével valamely csillagot beállítunk, akkor az a és c körnek b-u leolvasandó szöge a csillag óraszöge, a dioptrás vonalnak a c osztott körön b-hez viszonyított állása a csillag deklinációja. Ez alakban az A. a tökéletesebb equatoriális távcső előképe.”

Eratosthenes (Küréné, i. e. 276 – Alexandria, i. e. 194) hellén csillagász polihisztor találmánya, az armilláris szféra műszerként már befejezte pályafutását, de sokan úgy gondoljuk, hogy alkotója oktatási, szemléltetési célra konstruálta, műszerré jóval később fejlesztették. A középkorban Tycho de Brahe (Knudstrup, Dánia, 1546. december 14. – Benátky, (Prága mellett) Csehország, 1601. október 24.) dán csillagász számos, a képeken látható csillagdát, műszert, és modellt konstruált. Az itt látható rajzok az ő Astronomiae Instauratae Mechanica c. művéből16 valók, annak illusztrációi.
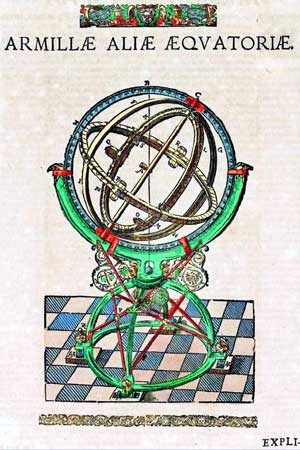


Az armilláris szférát a XIX-XX. századi magyar és külföldi tanszerkatalógusok mindegyikében megtalálhatjuk, szemléltetőeszköznek is jól bevált. A Naprendszer felépítésének, a Föld és bolygója, a Hold mozgásának demonstrálása mellett, a matematikai földrajzi fogalmaknak szinte mindegyike szemléltethető a segítségével. Egyéb földrajzi fogalmak és jelenségek szemléltetését is szolgálják: pl. geoid alak, tengely körüli forgás, szélességi és hosszúsági kör, Egyenlítő, Ráktérítő, Baktérítő, sarkkör, kezdő hosszúsági kör, holdfázis, holdtölte, újhold, nap- és holdfogyatkozás, etc.
A világhíres chemnitz-i Max Kohl17 cég kozmológiai taneszközei között, fellelhető armilláris szféra, éggömb, annak fontosabb köreit ábrázoló, gyűrűkből összeállított horizontárium, világóra, és több komplex modell is, de, miként majd látjuk, büszke lehet az egykori magyar tanszeripar is.


Az 1900-ban alapított magyar Marx és Mérei Tudományos Műszerek Gyára is kínál csillagászati eszközöket, a távcsövek mellett egy komplex kozmikus modellt. Az „Új készülék a mennyiségtani földrajz (mathematikai geografia) tanításához” sokoldalúsága metodikailag is figyelemre méltó. Az eszköz hiteles bemutatása az 1912. évi 9. sz. árjegyzék eredeti katalóguslapjai segítségével itt következik:


A készülékkel kapcsolatban érdemes megjegyezni, hogy a közismert, A távcső világa c. kézikönyvben,18 Schalk Gyula – aki valószínűleg nem ismerte a Marx és Mérei cég tanszereit – A csillaggömböktől a planetáriumokig c. fejezetében pontosan egy ilyen készüléket hiányolt, vagy fedezett fel: „Ezzel (t.i. az armilláris szférával) a – meridián síkja mentén fixált és fokbeosztással ellátott – két koncentrikus gyűrűvel közvetlenül mérhették az égitestek láthatár feletti magasságát, de meghatározhatták a napfordulókat és a Föld tengelyferdeségét is. A műszer – bár mérőműszer – alkalmas a főkörök szemléltetésére is. Ha pedig valaki egy kis korongot helyezett volna az elliptikagyűrűre, és azt megforgatta volna, bemutathatta volna az égbolt napi mozgása is. Egy – észak-dél irányú, tengely körüli – elforgatással pedig bemutatható lett volna az égbolt napi mozgása is.”
A középiskolák számára a Budapesten, 1819-ben alapított Calderoni Mű- és Tanszervállalat Részvénytársaság is forgalmazott a látszólagos égboltozat forgását és az égitestek látszólagos mozgását demonstráló Wislicenus-féle uranotrop19 készüléket:
A jövő taneszközei – látványos elektronikus szemléltetés a NET-en
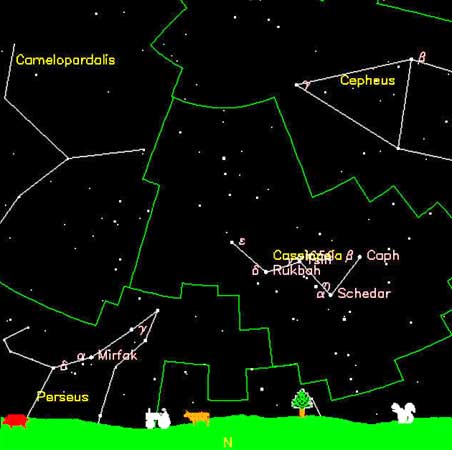
Az Interneten elérhető virtuális, interaktív planetáriumokig a csillagképeken, csillagabroszokon, armilláris szférákon, álló és mozgó csillaggömbökön, mechanikus planetáriumokon és csillagvetítőkön át vezet az út. Cikkünk elektronikus változatában jól érzékelhető lesz, hogy a csillagászati taneszközök legújabb, interaktív elektronikus generációja alapvetően új megoldásokat kínál. Létezik már több virtuális teleszkóp is, pl. a http://www.worldwidetelescope.org/Home.aspx, vagy a http://www.fourmilab.ch/yoursky. Ez utóbbi szerkesztője, a csillagász John Walker szerint, 2009. február 24-én, hajnali 3 óra 18 perckor ezt látom a Pilis lábánál, Ürömön az ablakomból kinézvén:

View toward horizon from 47°42’N 19°E, azimuth 0° (N) Tue 2009 Feb 24 3:18
Dolgom végeztével, ha ezt a cikket befejezném és kilépnék a havas teraszra, az égboltra tekintve, feliratok nélkül ezt látnám, ha nem zuhogna a hó:
Sky above 47°42’N 19°E (ÜRÖM) at Tue 2009 Feb 24 3:19 UTC
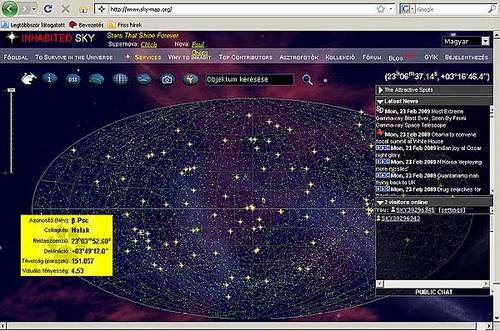
Az új lehetőségeknek kiváló példája még a www.sky-map.org címen elérhető csillagászati honlap. Az oldal egyszerre interaktív csillagtérkép és csillagászati wikipedia.

Katalógusa több millió csillagászati objektumot tartalmaz, így az egyik legkomolyabb, Interneten is elérhető gyűjteménynek számít, melynek elemei mind felkereshetők a nagyítható, Google Maps-hez hasonló térképen. Természetesen sokan úgy véljük, hogy a virtuális teleszkóp nem ér fel a természet közvetlen megfigyelésével, de jól kiegészíti klasszikus módszereinket.
{mosimage}
András Nádasi: Star messenger – special museum and modern astronomical instruments
On the occasion of the International Year of Astronomy the author describes the improvement of astronomy from Galilei and Kepler and displays the scientific results of the widely known Hungarian astronomer, Miksa Hell. In his study he deals with those astronomical instruments and cosmological educational aids that help to understand astrology. A number of items of his demanding study can be reached and supplemented through the web.
András Nádasi: Der Sternbote – besondere alte und moderne astronomische Instrumente
Anlässlich des Jahres der Astronomie schildert der Verfasser, zurückgreifend bis Galilei und Kepler, die Entwicklung der Sternkunde. Dann führt er die Ergebnisse der wissenschaftlichen Forschung des meistbekannten ungarischen Sternforschers Miksa Hell vor. In seinem Aufsatz befasst sich der Autor mit jenen astronomischen Geräten, kosmologischen Lehrmitteln, die zum besseren Verständnis der astronomischen Erscheinungen beitrugen. Der anspruchsvolle Aufsatz wird in der elektronischen Ausgabe der Zeitschrift ergänzt.
Jegyzetek:
1., Subic Simon kiváló, a „Természettan a felgymnásiumok és reáltanodák számára” c. tankönyvének csillagászati fejezete kezdődik ezzel az idézettel. A könyvet németből fordította és szerkeszté: Kreusz Krizosztom OSB – Kühn Rajmund OSB. Pest, Heckenast, 1866. 530 l. 1 sztl. lev.
2., Részletes programtájékoztató található a Magyar Kurír http://www.magyarkurir.hu/?m_op=view&id=25735 oldalán
3., Ilyen pl. az Eszterházy Károly Főiskola Természettudományi Pályaorientációs és Módszertani Központja által szervezett „Varázstorony Vetélkedő”. http://www.ektf.hu/varazstorony/index.html
4., http://www.tanszertar.hu/eken/2005_02/nadasi_0502.htm
5., http://www.derby.gov.uk/LeisureCulture/MuseumsGalleries/ArttreasureTheOrrery.htm
6., A Kepler törvények kiváló interaktív animációi találhatók a http://www.physics.sjsu.edu/tomley/Kepler12.html, http://www.physics.sjsu.edu/tomley/Kepler3.html oldalakon.
7., Hell Miksa a selmecbányai gimnázium elvégzése után, 1738-ban lépett be a jezsuita rendbe. A novíciátus elvégzése után Bécsben tanult filozófiát és természettudományokat. Kiváló eredményeire a Rendben is felfigyeltek. 1743-tól matematikát is tanult, 1744-től pedig csillagászati megfigyeléséket is közölt. 1745-től a jezsuita gimnázium tanára Lőcsén. 1748-52 között Bécsben tanult teológiát. 1751-ben szentelték pappá. Ekkor Besztercebányára került, ahonnan a nagyszombati csillagvizsgáló építését vezette. Nem sokkal ezután Kolozsváron is közreműködött az ottani csillagda építésének vezetésében. 1755-ben tudományos munkájának elismeréseképpen Mária Terézia kinevezte udvari csillagászává, s így megismerhette korának jelentős csillagászait. Hell sokat tett a magyar csillagászat fejlődéséért, közreműködött az egri és a budai obszervatórium megszervezésében. http://csillagaszattortenet.csillagaszat.hu/magyar_1819._sz._csillagaszata/szenkovits_hell_20060218.html
8., http://venuszatvonulas.load.hu/index.phtml?page=hell
9., Előbb jezsuita szerzetes, majd világi pap, matematikus, csillagász. Az egri felsőbb szeminárium, utóbb a Líceum matematika tanára. 1772—76 között Hell Miksa mellett Bécsben csillagászatot tanult. 1778-tól hat évig a Líceum csillagvizsgálójának vezetője. Ügyes észlelő, Jupiter-hold jelenségeket, csillagfedéseket, fogyatkozásokat figyelt meg, nagy pontossággal megállapította a csillagda földrajzi szélességét.
10., Kelényi B. Ottó: A magyar csillagászat története. Bp., 1930. pp. 16–22.
11., A Pallas Nagylexikon szerint a meridian, „a csillagászatban azon legnagyobb kör, mely az égi pólusokon és a megfigyelési hely tetőpontján (zenithjén) áthalad… . A Föld D.-e minden, a Föld forgási tengelyén átfektetett sik, mely a Föld felületén, ha azt gömbnek tekintjük, kört, ha pedig szferoidnak, akkor ellipszist szel ki. Az equator és ennek párhuzamos köreivel együtt a D.-ök a geografiai fokhálózatot szolgáltatják. De mig az equator igen alkalmas és a természettől magától kijelölt kezdetet nyujt a szélességi fokok olvasására, addig a D.-ök kiindulási pontja, az ugynevezett első v. kezdet D. teljesen önkényes. Ptolemaeos a kanári szigeteken áthaladó D.-t tekintette elsőnek, Eratosthenes Herkules oszlopain fektette át. Mercator a kanári Palma szigetén lévő St-Cruz kikötőjébe, a franciák végre Ferró szigetébe fektették oly módon, hogy a párisi csillagvizsgáló D.-e a mondott kezdet D.-től 20° 2” 30””-re kerül keletre. E helyett közmegegyezés folytán a kezdő D.-t pontosan 20°-kal teszik nyugotra a párisi meridiántól, úgy hogy tulajdonképen, bár álarcban, mégis a párisi szerepelt elsőnek. Most, midőn a nemzetközi első délkör kérdése még véglegesen eldöntve nincsen, különösen Ferro, Greenwich, Páris, Berlin és Washington szerepel kezdő D. gyanánt. A számoló csillagász kivétel nélkül a berlini meridiánhoz ragaszkodik, mert az ottani csillagvizsgáló szolgáltatja a pályameghatározásokhoz szükséges legkényelmesebb és legteljesebb táblázatokat, a régibb geografia Ferrot pártolja, az ujabb haladás és az európai majd az összes hajózás, továbbá a világ- v. zónaidő Greenwichet választotta.”
12., Az azimut (arab, tetőponti szög), azon szög, melyet valamely (csillagon v. földi objektumon áthaladó) magassági kör képez a meridiánnal. A csillagászok a délponttól kiindulva nyugaton, Északon, keleten át 0°-tól 360°-ig számítják, a geodéták és (kivételesen a csillagászok is) északból kiindulva keleten, délen, nyugaton át ugyancsak 360°-ig. Az azimut mértéke a horizon vagy valamely almukantarat azon íve, mely a csillag vertikális köre és a délkör között fekszik. Meghatározására szolgál az altazimut a teodolit v. egyszerűbb esetben a mágneses deklináció tekintetbevételével a boussola.
13., A Csillagászati Múzeumot az 1960-as években Dr. Zétényi Endre, az Egri Pedagógiai Főiskola Földrajz Tanszékének docense, szervezte meg, aki visszaszerezte az Egerből elvitt muzeális tárgyakat, helyreállíttatta a Csillagda nyugati termében föllelt linea meridionalist, megjavíttatta a kupola tükrös távcsövét, és számos technikatörténeti tárggyal gazdagította a múzeumot. Munkásságát emléktábla idézi az egri Lyceum falán.
14., http://www.ektf.hu/ujweb/index.php?page=96
15., A Cosmodyesse IV típusú planetárium a francia R.S.A. Cosmos cég legújabb fejlesztése, csillagvetítője lehetővé teszi, hogy a 6m átmérőjű kupola felületére vetítse a csillagos ég látványát a Föld bármely pontjáról.
16., A Kalocsai Főszékesegyházi Könyvtár http://www.asztrik.hu/konyvtar/konyvek/konyvek.htm#4 honlapján a teljes könyv megtekinthető.
17., A világhírűvé vált német Max Kohl Finommechanikai és Elektrotechnikai Műhelyt csak 1876-ban alapították, több évtizeddel a magyar Calderoni Vállalat megalapítása után. Gyártmányait sok iskolai szertár és a Max Kohl Múzeum őrzi.
18., Kulin György – Róka Gedeon (szerk.): A távcső világa. Gondolat Kiadó, Budapest, 1975. 512. l.
19., Walter Friedrich Wislicenus (Halberstadt, 1859. november 5. – Strassbourg, 1905. október 3.) német csillagász, 1883-tól, a Strassbourgi Obszervatórium munkatársaként számos népszerű-tudományos csillagászati előadást tartott. 1888-tól haláláig a Straßburg Egyetem professzora. Legjelentősebb műve, az általa indított Csillagászati Évkönyv (Astronomischer Jahresbericht, Astronomisches Rechen-Institut, Heidelberg), amely 1899-1969-ig jelent meg. A sorozat elérhető a http://www.ari.uni-heidelberg.de/publikationen/ajb/index.htm oldalon. Az „Uranotrop – egy demonstrációs eszköz: leírás és használati utasítás” c. füzete 1901-ben jelent meg, Strassbourgban.
A Könyv és Nevelés 2009/1. számában (http://www.tanszertar.hu/eken/2009_01/na_0901.htm) megjelent cikk másodközlése