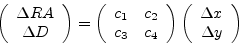Az égi rektaszcenzió-deklináció koordinátapárok és a képen belüli x-y pixelkoordináta-párok közötti átváltást, azaz a két koordinátarendszer egymás közötti transzformációját a fotografikus érából eredő elnevezésű lemezkonstansok mátrixával valósíthatjuk meg. Ennek legegyszerűbb formája lineáris átváltást tételez fel, amit a következő alakú egyenletek írnak le:
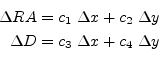
Azaz vektor- és mátrixalakban:
Itt ΔRA és Δδ egy képen tetszőlegesen kiválasztott referenciaponttól mért rektaszcenzió- és deklináció-különbség, Δx és Δy pedig az ugyanettől mért x és y irányú pixelkoordináta-különbség. Három csillag a minimum, ami megoldhatóvá teszi a lemezkonstansokra vonatkozó többismeretlenes egyenletrendszert.
Ha a három referenciapont a 0, 1 és 2 jelölésű csillag, akkor tekintsük az alábbi különbségeket:
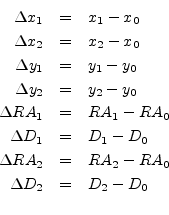
Ezek mindegyike ismert mennyiség, hiszen a referenciacsillagok azért referenciák, mert mindent tudunk róluk.
Ezután a transzformációs egyenletek kiírva:
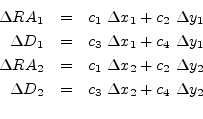
Négy egyenlet, négy ismeretlen (c1, c2, c3 és c4), azaz a rendszer megoldható, a lemezkonstansok kiszámíthatók.
Ezek után egy tetszőleges (X,Y) pixelkoordináta átváltása égi koordinátákra:
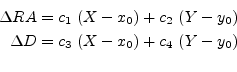
Amiből a pont teljes égi koordinátái:
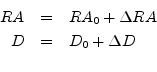
A vázolt eljárás sok esetben elegendően pontos, ám nagy látómezők (több tíz ívperc) esetén az ívmásodperces pontosságú asztrometriához két irányban is lehet (kell) javítani a számításokat:
1. magasabb rendű tagokat is beveszünk a transzformációba, azaz konstansszor (dx)2, (dy)2, dxdy tagokat, melyek újabb lemezkonstansok definiálását vonják maguk után;
2. több referenciacsillagra van szükség az egyenletrendszerek megoldhatóságához;
2.5. egész sok referencacsillag esetén pedig már nem is megoldjuk az egyenletrendszert, hanem legkisebb négyzetes illesztéssel kiszámítjuk a legjobb illeszkedést adó lemezkonstansokat.
A témában pár éve a Meteorban is megjelent egy cikk, aminek elektronikus változata itt olvasható el.